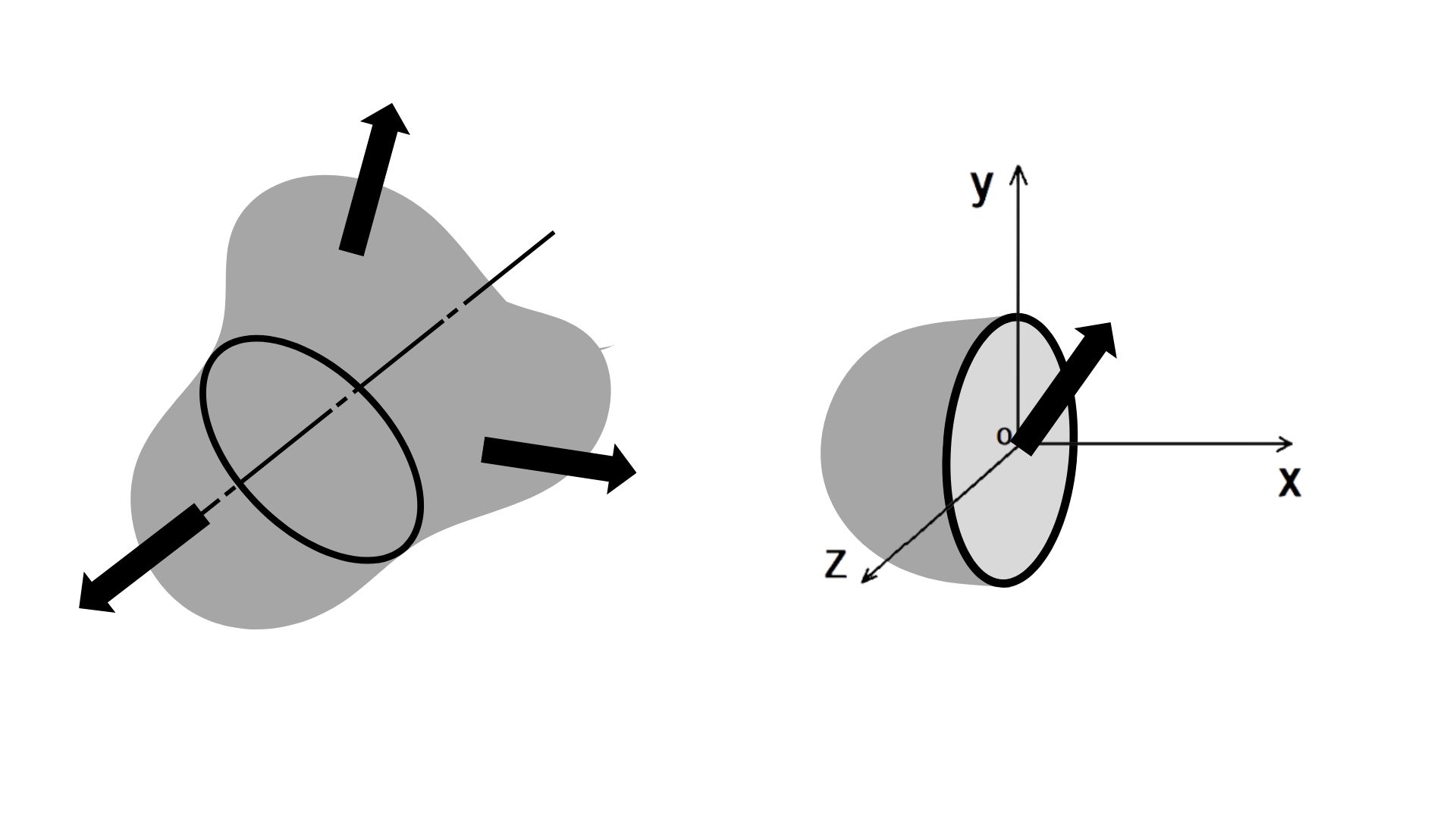
-材料力学の意義
材料力学は内部の状態について検討するものであるが、その検討対象は2種類ある
・強度
1つは破壊防止である。構造物が稼働中に過大に荷重を受けると破壊が発生する。この破壊を防止するためには、材料や構造物の強度を高める必要があり、そのために行うのが強度検討である。材料の破壊を測る指標として一般的に用いられている量が、応力である。
・剛性
もう1つは構造物の変形防止である。構造物が荷重を受けると、構造物に変形が発生する。この変形が過大にならないように防止するには、材料や構造物の剛性を高める必要があり、そのために行うのが剛性検討である。剛性が低いと変形しやすくなる。
構造物の変形量や破壊しないかをシミュレーションするには、構造物内部の応力状態を正確に記述する必要がある。今回は、微小変形の範囲内での弾性体に焦点を当てて、CAEの構造解析で弾性体を表現するための構成式を解説していく。
-材料力学の制約、線形性
材料力学を考える上で、力とモーメントには釣り合いの状態になければならないという制約がある。力とモーメントが釣り合っているとは、全ての力とモーメントのそれぞれの和は必ず0になる。
また、CAEをする上で大切になる仮定が、線形性である。線形性とは、作用量と発生量が全て比例する状態であり、途中経過は無関係で最初と最後の状態だけで決まる特性のことである。厳密に見た場合では、線形でなくても近似的に線形とみなせる現象であるなら、線形として扱うことが多い。そのためCAEでは、微小な変形に対して用いられることが一般的である。
このような仮定が適用できる物体を「弾性体」という。
弾性体の構造解析に用いられる構成式は、「応力の定義式」「ひずみの定義式」「応力-ひずみ関係式」の3つである。
-応力・ひずみの定義
材料力学の最も基本となる概念が、応力とひずみである。
応力の定義
「応力」とは、面に対して定義されるものである。力が釣り合った状態の物体の断面を考える。断面には、隠した部分の合力が作用している。その合力に対して、破断されまいと反対方向に力が発生して釣り合っている状態になる。この反対方向に作用する力を断面積で割ったものが「応力」である。「応力」の単位は、[\(Pa\)]（パスカル）、または、[\(N/m^2\)]である。材料力学の分野では、[\(MPa\)]（メガパスカル）または、[\(N/mm^2\)]を用いることが多い。（[\(M\)]（メガ）とは、\(10^6\)を意味する接頭語である。）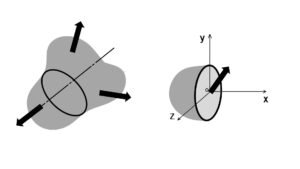
$$\sigma=F/A$$
ただし、\(\sigma\) は応力、\(F\) は荷重、\(A\) は断面積である。
断面に対して垂直に働く成分「垂直応力」と、平行に働く成分「せん断応力」がある。
$$\sigma_x=F_x/A$$
$$\tau_{xy,xz}=F_{xy,xz}/A$$
ただし、\(\sigma_x\) は垂直応力、\(\tau_{xy,xz}\) はせん断応力、\(F_x\) は 荷重の\(X\)成分、\(F_{xy,xz}\) は 荷重の\(Y\)成分及び\(Z\)成分である。
ひずみの定義
次に、「ひずみ」とは、力が作用した時の棒の元の長さと伸びた長さの割合である。力の方向に伸びた量の割合が「縦ひずみ」、力に垂直な方向に縮んだ割合が「横ひずみ」である。ひずみの単位は、無次元である。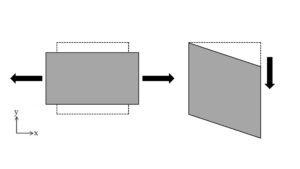
$$\epsilon_x=\delta_x/l$$
ただし、\(\epsilon_x\) は縦ひずみ、\(\delta_x\) は伸びた量、\(l\) は元の長さである。
$$\epsilon_y=\delta_y/h$$
ただし、\(\epsilon_y\) は横ひずみ、\(\delta_y\) は縮んだ量、\(h\) は元の幅である。
この縦ひずみ\(\epsilon_x\) と横ひずみ\(\epsilon_y\) の比率は、材料によって一定であることが知られている。この比率を「ポアソン比」という。$$\nu=\left|\frac{\epsilon_y}{\epsilon_x}\right|$$
せん断力（断面に平行な力）による平行四辺形状の変形を「せん断変形」と呼び、元の長さとずれ量の割合が「せん断ひずみ」である。
$$\gamma=\delta_y/l$$
垂直応力及び縦ひずみの値が、正の場合は「引張」、負の場合は「圧縮」を意味する。
また、せん断応力及びせん断ひずみの正負については、物理的な意味は特にない。座標系によって正負の値が反転することがある。
フックの法則
微小変形では、垂直応力と縦ひずみは比例の関係にある。これを「フックの法則」といい、比例定数を「縦弾性係数」（「ヤング率」）\(E\) という。縦弾性係数は、材料固有の値であり、単位は、応力と同じ[\(Pa\)]（パスカル）、または、[\(N/m^2\)]である。一般的には、[\(GPa\)]（ギガパスカル）を用いることが多い。（[\(G\)]（ギガ）とは、\(10^9\)を意味する接頭語である。）
$$\sigma_x=\epsilon_xE$$
また、せん断応力とせん断ひずみに間にも「フックの法則」が成り立つ。この時の比例定数を「横弾性係数」\(G\)という。
$$\tau_{xy,xz}=\gamma G$$
「縦弾性係数」\(E\)と「横弾性係数」\(G\)の間には、金属の場合、次の関係式が成り立つ。
$$E=2(1+\nu) G$$
CAEのプログラムの多くは、\(E\)と\(\nu\)のみを入力し、\(G\)は上式から自動で計算してくれるようになっている。
-応力の定義式（応力の釣り合い方程式）
応力の定義式を導出するにあたって、実際の構造物は三次元であるが、まずは簡単のため二次元での応力の定義式を導出する。\(xy\)座標系にある微小四変形を考える。「微小」意味するところは、四変形に作用する力の分布が一様であると想定できることである。この微小四変形の各辺に垂直応力とせん断応力が作用した場合の力の釣り合い式を立てる。応力は、力を断面積で割った値なので、応力に微小四変形の長さをかけることで、力を出すことができる。
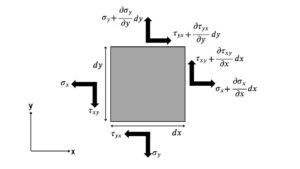
\(x\)方向の力の釣り合い式
$$\left(\sigma_x+\frac{\partial \sigma_x}{\partial x}dx\right)dy – \sigma_xdy + \left(\tau_{yx}+\frac{\partial \tau_{yx}}{\partial y}dy\right)dx – \tau_{yx}dx+ F_xdxdy = 0$$
\(y\)方向の力の釣り合い式
$$\left(\sigma_y+\frac{\partial \sigma_y}{\partial y}dy\right)dx – \sigma_ydx + \left(\tau_{xy}+\frac{\partial \tau_{xy}}{\partial x}dx\right)dy – \tau_{xy}dy + F_ydxdy = 0$$
ただし、\(F_x\)、\(F_y\)は微小四変形に働く外力の\(x\)成分と\(y\)成分である。
\(x\)方向の力の釣り合い式の第一項について説明する。カッコ内は、\(\sigma_x\)をテイラー展開により二次近似した表現である。その他のカッコ内も同様である。
これらの2つの釣り合い式を整理すると、
$$\frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{yx}}{\partial y}+ F_x = 0$$
$$\frac{\partial \sigma_y}{\partial y} + \frac{\partial \tau_{xy}}{\partial x}+ F_y = 0$$
となる。
次に、四変形中心回りのモーメントの釣り合い式を考える。中心を通る直線状に垂直応力が作用しているため、垂直応力によるモーメントはゼロである。したがって、
$$\left(\tau_{yx} + \frac{\partial \tau_{yx}}{\partial y}dy\right)\frac{1}{2}dxdy + \tau_{yx}\frac{1}{2}dxdy – \left(\tau_{xy}+\frac{\partial \tau_{xy}}{\partial x}dx\right)\frac{1}{2}dxdy – \tau_{xy}\frac{1}{2}dxdy = 0$$
この式が成り立つには、
$$\tau_{yx} = \tau_{xy}$$
である必要がある。つまり、せん断応力は対称性を持っているということになる。
三次元の場合も、二次元と同様に力の釣り合い式から、次の式が導き出せる。
\begin{align*}
\frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z} + F_x &= 0 \\
\frac{\partial \tau_{xy}}{\partial x} + \frac{\partial \sigma_y}{\partial y} + \frac{\partial \tau_{zy}}{\partial z} + F_y &= 0 \\
\frac{\partial \tau_{xz}}{\partial x} + \frac{\partial \tau_{yz}}{\partial y} + \frac{\partial \sigma_z}{\partial z} + F_z &= 0
\end{align*}
-ひずみの定義式
応力の定義式を導出した時と同様に、まずは二次元でのひずみの定義式を導出する。\(xy\)座標系にある微小四変形を変形させた時のひずみを考える。
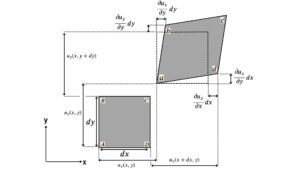
ひずみは、元の長さと伸びた量の割合なので、\(x\)方向のひずみを導出すると、
\begin{align*}
\epsilon_x &= \frac{\overline{ad}-\overline{AD}}{dx}\\
&= \frac{u_x\left(x+dx,y\right) + dx – u_x\left(x,y\right)}{dx}\\
&= \frac{\frac{\partial u_x}{\partial x}dx + dx – dx}{dx}\\
&= \frac{\partial u_x}{\partial x}\\
\end{align*}
となる。
\(y\)方向のひずみについても同様に導出する。
\begin{align*}
\epsilon_y &= \frac{\overline{ab}-\overline{AB}}{dy}\\
&= \frac{u_y\left(x,y+dy\right) + dy – u_y\left(x,y\right)}{dy}\\
&= \frac{\frac{\partial u_y}{\partial y}dy + dy – dy}{dy}\\
&= \frac{\partial u_y}{\partial y}\\
\end{align*}
次に、せん断ひずみについて導出する。せん断ひずみは、元の長さとずれ量の割合で求められるので、
\begin{align*}
\gamma_{xy} &= \frac{\frac{\partial u_x}{\partial y}dx}{dx}+\frac{\frac{\partial u_y}{\partial x}dy}{dy}\\
&= \frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x}\\
\end{align*}
となる。
三次元の場合も、二次元と同様にひずみの定義から、次の式が導き出せる。
\begin{align*}
\epsilon_x &= \frac{\partial u_x}{\partial x} \\
\epsilon_y &= \frac{\partial u_y}{\partial y} \\
\epsilon_z &= \frac{\partial u_z}{\partial z} \\
\gamma_{xy} &= \frac{\partial u_x}{\partial y} + \frac{\partial u_y}{\partial x} \\
\gamma_{yz} &= \frac{\partial u_y}{\partial z} + \frac{\partial u_z}{\partial y} \\
\gamma_{zx} &= \frac{\partial u_z}{\partial x} + \frac{\partial u_x}{\partial z}
\end{align*}
-フックの法則（応力とひずみの関係）
弾性体では、応力とひずみの間にフックの法則\(\left(\sigma=E\epsilon\right)\)が成立する。まずは、\(xy\)座標系での二次元における\(x\)方向のフックの法則を見てみよう。\(x\)軸に垂直な断面に作用する垂直応力\(\sigma_x\)による縦ひずみと\(y\)軸に垂直な断面に作用する垂直応力\(\sigma_y\)による横ひずみが同時に発生する。縦ひずみは\(x\)軸の正方向に、横ひずみは負の方向に発生する。横ひずみには、ポアソン比\(\nu\)をかける必要があることに注意が必要である。
$$\epsilon_x = \frac{1}{E}\left(\sigma_x-\nu\sigma_y\right)$$
\(y\)方向に関しても同様である。
$$\epsilon_y = \frac{1}{E}\left(-\nu\sigma_x+\sigma_y\right)$$
せん断ひずみとせん断応力との間で成立するフックの法則は、横弾性係数を用いて、次の式で表現される。
$$\gamma_{xy} = \frac{1}{G}\tau_{xy}$$
これらの式を三次元に拡張すると、
\begin{align*}
\epsilon_x &= \frac{1}{E}\left\{\sigma_x-\nu\left(\sigma_y+\sigma_z\right)\right\}\\
\epsilon_y &= \frac{1}{E}\left\{\sigma_y-\nu\left(\sigma_x+\sigma_z\right)\right\}\\
\epsilon_z &= \frac{1}{E}\left\{\sigma_z-\nu\left(\sigma_x+\sigma_y\right)\right\} \\
\gamma_{xy} &= \frac{1}{G}\tau_{xy}\\
\gamma_{yz} &= \frac{1}{G}\tau_{yz}\\
\gamma_{zx} &= \frac{1}{G}\tau_{zx}
\end{align*}
上式が実際に使用される場合、特にCAEの内部ではひずみから応力を求めることが多いので、その形も示しておく。
\begin{align*}
\sigma_x &= \frac{E}{1-\nu^2}\left(\epsilon_x+\nu\epsilon_y+\nu\epsilon_z\right)\\
\sigma_y &= \frac{E}{1-\nu^2}\left(\nu\epsilon_x+\epsilon_y+\nu\epsilon_z\right)\\
\sigma_z &= \frac{E}{1-\nu^2}\left(\nu\epsilon_x+\nu\epsilon_y+\epsilon_z\right)\\
\tau_{xy} &= G\gamma_{xy}\\
\tau_{yz} &= G\gamma_{yz}\\
\tau_{zx} &= G\gamma_{zx}\\
\end{align*}
CAEの便宜上、ベクトルとマトリクスの形で表現する。左辺を「応力ベクトル」、右辺のマトリクスを「\(D\)マトリクス」、ベクトルを「ひずみベクトル」と呼ぶ。
\begin{equation*}
\left\{
\begin{array}{c}
\sigma_x \\
\sigma_y \\
\sigma_z \\
\tau_{xy} \\
\tau_{yz} \\
\tau_{zx}
\end{array}
\right\}=
\frac{E}{1-\nu^2}
\left[
\begin{array}{cccccc}
1 & \nu & \nu & 0 & 0 & 0 \\
\nu & 1 & \nu & 0 & 0 & 0 \\
\nu & \nu & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{1-\nu}{2} & 0 & 0 \\
0 & 0 & 0 & 0 & \frac{1-\nu}{2} & 0 \\
0 & 0 & 0 & 0 & 0 & \frac{1-\nu}{2}
\end{array}
\right]
\left\{
\begin{array}{c}
\epsilon_x \\
\epsilon_y \\
\epsilon_z \\
\gamma_{xy} \\
\gamma_{yz} \\
\gamma_{zx}
\end{array}
\right\}
\end{equation*}
ここで、\(E=2(1+\nu) G\)の関係式を用いている。
