機械設計に携わっているエンジニアの方々には、CAEやFEMという言葉をよく耳にするかと思います。解析を実行すると構造物の応力が可視化され、デジタル上で設計のフィードバックができる便利なツールです。しかし、その中身を理解して使っている人はどれくらいでしょうか?
本稿では、アカデミックな内容を割愛し、構造解析の本質的な部分のみを解説していく。
-CAEとは?
コンピュータを技術開発に利用する手法をComputer Aided Engineering(CAE)といい、構造解析や熱伝導解析などもこれに含まれている。
CAEの基となる分野が計算力学であり、下記のようにさまざまな分野においてその応用が活発に研究されている。
・固体力学(材料力学、構造力学、地盤力学etc)
・流体力学(流体機械学、空気力学、気象学etc)
・移動現象学(熱伝達、物質移動、反応工学)
・電磁気学、音響学・・・
物理学、特に力学理論に裏付けられたシミュレーションを行う主な利点として、コスト的問題の軽減化、品質的問題の向上、時間的問題の短縮化が挙げられる。
CAEはCADよりも古くから普及したツールであり、実測に置き換わるような検証手段としてその存在価値を遺憾なく発揮してきた。また、以前のCAEは専門知識と経験を持った解析専任者でしか扱えなかったが、昨今は操作が簡単になって一般の設計者でもCAEを使って解析できるようになってきた。
-CAEの将来性
コンピュータ支援工学(CAE)の未来は、AIの進化、製品の複雑化、開発期間の短縮、そして労働力不足という課題に対応する形で明るい展望を示しています。AIの普及により、CAEシステムはより高度な解析と効率的な設計提案が可能になり、複雑なマルチマテリアル製品や電動化された製品の設計も、精度高く迅速に行えるようになります。
短期間での製品開発が求められる中、CAEはシミュレーションを通じて設計の試行錯誤を大幅に減らし、開発スピードの加速を実現します。また、労働人口の減少が進む中で、CAEは設計者の負担を軽減し、より少ない人員でより多くの仕事をこなせるよう支援します。このように、CAEは技術的進歩と社会的ニーズの両方に対応し、今後も多方面での重要性を増していくと予想されます。
-CAEの問題点、注意点
CAEを導入した企業の約半数では、解放されるはずの強度トラブルに相変わらず悩まされ続けているのが実情である。
CAEを利用して計算することが容易な時代であるが、コンピュータが必ずしも「正しい」結果を出力しているとは限らない。その結果を見て、人が正しい判断ができるという保証もない。
CAEが出力する結果を「正しく」理解するためには、CAEがブラックボックスであってはならない。コンピュータがどのような計算を行い、ひずみや応力がどのように計算されているかを理解することによって、「正しい」CAEが実現される。
-有限要素法とは
CAEの構造解析では、フックの法則\(\left(F=k\delta\right)\)を用いて表現された方程式を解いて応力を求めているが、ここで問題となるのが、\(k\)の値である。梁構造だと、1本の梁の力と変位の関係式が分かっているので、それらを連立方程式で解けば良い。しかし、一般形状の構造物では、簡単に決めることができない。そこで、次に示すような考え方で決められた方法が考案された。これが「有限要素法(Finite Element Method:FEM)」である。
①構造物を要素と呼ぶ単純で小さい形状に領域を分割する
②要素同士は節点と呼ぶ点を通じて力や変位の伝達を行う
③要素内部の変位分布を表すために、簡単な関数形を(変位関数)を仮定する
④変位関数をもとに、要素に所属する節点間のばね定数を決定する
⑤分布荷重はこれと等価な節点荷重に換算する
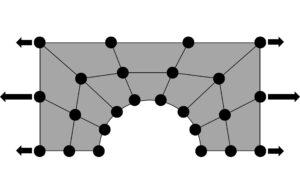
つまり、有限要素法とは、構造物を単純な形状の集合体と見なし、各要素の節点の変位量を求めることで、構造物全体の変形を求める方法である。構造物を単純な形状に分けることを「離散化」という。離散化とは、連続した関数などを有限な領域として表現する手法のことである。
-計算の流れ
有限要素法を用いて、構造物の変形や応力を求める流れを順に説明する。CAEの構造解析で解かれている式を解説するよりも、先に計算全体の流れを知っておいた方が、式に対する理解がスムーズに進むので、まずは、計算全体の流れを理解していただきたい。
1. モデル情報を読み込む、物性値や境界条件を定義する
計算した構造物のモデル、構造物に働く荷重や拘束条件を決める。構造解析では、力の釣り合い式を解いているので、構造物が並進運動や回転運動をしていないことが前提となる。そのため、拘束条件には細心の注意が必要である。
2. 材料ごとに\(D\)マトリクス(剛性マトリクス)を作成する
材料のヤング率とポアソン比を定義し、剛性マトリクスを作成します。右辺のマトリクスを「\(D\)マトリクス」と呼ぶ。これは、材料によって一意に決まるマトリクスである。
\begin{equation*}
\left\{
\begin{array}{c}
\sigma_x \\
\sigma_y \\
\sigma_z \\
\tau_{xy} \\
\tau_{yz} \\
\tau_{zx}
\end{array}
\right\}=
\frac{E}{1-\nu^2}
\left[
\begin{array}{cccccc}
1 & \nu & \nu & 0 & 0 & 0 \\
\nu & 1 & \nu & 0 & 0 & 0 \\
\nu & \nu & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{1-\nu}{2} & 0 & 0 \\
0 & 0 & 0 & 0 & \frac{1-\nu}{2} & 0 \\
0 & 0 & 0 & 0 & 0 & \frac{1-\nu}{2}
\end{array}
\right]
\left\{
\begin{array}{c}
\epsilon_x \\
\epsilon_y \\
\epsilon_z \\
\gamma_{xy} \\
\gamma_{yz} \\
\gamma_{zx}
\end{array}
\right\}
\end{equation*}
⏬\(D\)マトリクスの詳細は下記リンクから⏬
https://mekaisroman.com/fem-make/31/
3. 要素ごとに\(B\)マトリクス(形状関数)を作成する
要素の内の変位分布を表現するために「\(B\)マトリクス」を作成する。先ほどの図を見て分かる通り、構造物を離散化すると、同じ四辺形でも形状の異なる要素が出てくる。形状の異なる要素内の変位分布を同じ関数形で計算するために用いられるのが「\(B\)マトリクス」である。「\(B\)マトリクス」は四辺形要素や三角形要素によって異なる。四辺形の「\(B\)マトリクス」の具体的な式を載せておく。
\begin{equation*}
\mathbf{B}=
\left[
\begin{array}{cccccc}
\frac{\partial N_1}{\partial x} & 0 & \frac{\partial N_2}{\partial x} & 0 & \frac{\partial N_3}{\partial x} & 0 \\
0 & \frac{\partial N_1}{\partial y} & 0 & \frac{\partial N_2}{\partial y} & 0 & \frac{\partial N_3}{\partial y} \\
\frac{\partial N_1}{\partial y} & \frac{\partial N_1}{\partial x} & \frac{\partial N_2}{\partial y} & \frac{\partial N_2}{\partial x} & \frac{\partial N_3}{\partial y} & \frac{\partial N_3}{\partial x}
\end{array}
\right]
\end{equation*}
$$N_1 = \frac{1}{2}\left(1 – \xi\right)\left(1 – \eta\right)$$
$$N_2 = \frac{1}{2}\left(1 + \xi\right)\left(1 – \eta\right)$$
$$N_3 = \frac{1}{2}\left(1 + \xi\right)\left(1 + \eta\right)$$
$$N_4 = \frac{1}{2}\left(1 – \xi\right)\left(1 + \eta\right)$$
⏬\(B\)マトリクスの詳細は下記リンクから⏬
https://mekaisroman.com/fem-make/166/
4. 要素ごとに要素剛性マトリクスを作成する
各要素の荷重と変位の関係は、
$$\left[\mathbf{K_e}\right]\left\{\mathbf{u}\right\} – \left\{\mathbf{f}\right\} = 0$$
という基本式として表される。ただし、\(\left\{\mathbf{u}\right\}\)は節点変位、\(\left\{\mathbf{f}\right\}\)は節点荷重である。
\(\left[\mathbf{K_e}\right]\)を「要素剛性マトリクス」といい、vマトリクスと\(B\)マトリクスを要素内で積分することで求めることができる。
$$\left[\mathbf{K_e}\right]\equiv\int_V\left[\mathbf{B}\right]^T\left[\mathbf{D}\right]^T\left[\mathbf{B}\right]dV$$
\(D\)マトリクスは、ヤング率とポアソン比で構成されており、物体内で変化しないので定数マトリクスである。一方、\(B\)マトリクスは、要素の形状によって変化するが要素内で変化するものではないので、やはり定数マトリクスである。したがって、\(D\)マトリクスと\(B\)マトリクスで構成されている要素剛性マトリクスも当然ながら定数マトリクスである。
5. 全ての要素剛性マトリクスを足し合わせ全体剛性マトリクスを作成する
全ての要素剛性マトリクスを求めたら、それらを1つにまとめて「全体剛性マトリクス」を作成する。
要素剛性マトリクスは、要素ごとに独立しており、まだ要素同士が繋がっていない状態である。要素が結合された構造物の全剛性を得るには、節点を通して要素剛性マトリクス同士を結び付け、全体として1つのマトリクスに組み上げる必要がある。要素剛性マトリクスの成分は、対応する要素内節点同士の剛性の関係を表している。これらの成分を全体剛性マトリクスの対応する成分に当てはめながら、全ての要素の剛性マトリクス成分を足し合わせていく。
6. 全体剛性マトリクス、境界条件から連立方程式を作成する
次は、全体変位ベクトル\(\left\{\mathbf{U}\right\}\)と全体荷重ベクトル\(\left\{\mathbf{F}\right\}\)を作成する。全体変位ベクトル\(\left\{\mathbf{U}\right\}\)と全体荷重ベクトル\(\left\{\mathbf{F}\right\}\)は、成分が節点自由度に対応したベクトルであり、節点数×自由度の成分を持っている。6節点からなるモデルで、自由度が\(x\)成分と\(y\)成分である場合は、全体変位ベクトル\(\left\{\mathbf{U}\right\}\)と全体荷重ベクトル\(\left\{\mathbf{F}\right\}\)は、12成分となる。全体変位ベクトル\(\left\{\mathbf{U}\right\}\)と全体荷重ベクトル\(\left\{\mathbf{F}\right\}\)と全体剛性ベクトル\(\left[\mathbf{K}\right]\)からなる連立方程式を解いて、変位を求める。
$$\left[\mathbf{K}\right]\left\{\mathbf{U}\right\} – \left\{\mathbf{F}\right\} = 0$$
7. 連立方程式を解いて、全節点の変位ベクトルを計算する
全体剛性マトリクス、全体変位ベクトル、全体荷重ベクトルからなる連立方程式を作ることができたが、まだ方程式を解くことはできない。方程式の変数である変位ベクトルの成分の内、拘束や強制変位がある成分は既知であるが、連立方程式を一意で解くためには、方程式の数と未知数の数が等しくなくてはならない。そのため、方程式の既知成分に対応する部分の影響を除去する必要がある。
簡単な方程式で見てみよう。
\begin{equation*}
\left[
\begin{array}{cccccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{array}
\right]
\left\{
\begin{array}{c}
u_1 \\
u_2 \\
u_3 \\
\end{array}
\right\}=
\left\{
\begin{array}{c}
f_1 \\
f_2 \\
f_3 \\
\end{array}
\right\}
\end{equation*}
未知数3つの連立一次方程式である。分解すると
$$\left\{\array{
a_{11}u_1 + a_{12}u_2 + a_{13}u_3 = f_1\\
a_{21}u_1 + a_{22}u_2 + a_{23}u_3 = f_2\\
a_{31}u_1 + a_{32}u_2 + a_{33}u_3 = f_3
}\right.$$
このうち\(u_2=\overline{u}\)とすると、
$$\left\{\array{
a_{11}u_1 + a_{12}\overline{u} + a_{13}u_3 = f_1\\
a_{31}u_1 + a_{32}\overline{u} + a_{33}u_3 = f_3
}\right.$$
$$\left\{\array{
a_{11}u_1 + a_{13}u_3 = f_1 – a_{12}\overline{u}\\
a_{31}u_1 + a_{33}u_3 = f_3 – a_{32}\overline{u}
}\right.$$
とすれば、未知数2つと方程式2となり、連立方程式を解くことができる。
これらをマトリクスとベクトルで表現すると、
\begin{equation*}
\left[
\begin{array}{cccccc}
a_{11} & 0 & a_{13} \\
0 & 1 & 0 \\
a_{31} & 0 & a_{33} \\
\end{array}
\right]
\left\{
\begin{array}{c}
u_1 \\
u_2 \\
u_3 \\
\end{array}
\right\}=
\left\{
\begin{array}{c}
f_1 – a_{12}\overline{u}\\
\overline{u} \\
f_3 – a_{32}\overline{u}\\
\end{array}
\right\}
\end{equation*}
となる。
連立方程式を解く方法には、大きく分類すると、直接法と反復法がある。直接法では、行と列の演算によりマトリクスを変形しながら解を導いていく。一方、反復法では、解を推定して繰り返し計算により精密な解に漸近させる方法である。直接法の中でもっとも一般的な方法は、ガウスの消去法である。ガウスの消去法はマトリクスの下三角部の成分を0とし、上三角行列とした後で、求められた変数を下から上に代入していく方法である。
⏬連立方程式の解法の詳細は下記リンクから⏬
https://mekaisroman.com/fem-make/279/
8. 各節点の変位ベクトルから、各要素のひずみ・応力を計算する
連立方程式から求められた各節点の変位ベクトルから、各要素のひずみと応力を計算する。
ひずみは、
$$\left\{\mathbf{\epsilon}\right\} = \left[\mathbf{B}\right]\left\{\mathbf{u}\right\}$$
を使って求めることができる。\(\left[\mathbf{B}\right]\)はそれぞれの要素の\(B\)マトリクス、\(\left\{\mathbf{u}\right\}\)は各要素内の節点変位ベクトルである。ひずみは要素ごとに計算することになり、結果として得られるひずみは、要素のひずみとなる。
応力は、
$$\left\{\mathbf{\sigma}\right\} = \left[\mathbf{D}\right]\left\{\mathbf{\epsilon}\right\}$$
の関係から求めることができる。応力もひずみ同様、要素ごとに計算することになり、結果として得られる応力は、要素の応力となる。