-場の微分
場所によって値やベクトルが異なるときに「場」という概念が用いられる。例えば、温度は場所によって異なるので「温度場」、流れに対しては「流速場」、応力に対しては「応力場」という。この時、場所によって異なるものの違いによって、2つに大別できる。
スカラー場
スカラーとは、方向を持たない値のことである。空間内にある領域で定義されたスカラーの関数が存在するとき、この領域と関数をあわせて、「スカラー場」という。物理においては、温度や圧力などがこれに対応する。
ベクトル場
ベクトルとは、方向と大きさを持つ値のことである。空間内にある領域で定義されたベクトル関数が存在するとき、この領域と関数をあわせて、「ベクトル場」という。物理においては、応力や流れなどがこれに対応する。
(スカラー場の)勾配
スカラー場\(f(x,y,z)\)において、次のようなベクトルを「勾配」という。
$$\mathrm{grad} f = \displaystyle\frac{\partial f}{\partial x}\mathbf{i} + \displaystyle\frac{\partial f}{\partial y}\mathbf{j} + \displaystyle\frac{\partial f}{\partial z}\mathbf{k}\tag{1}$$
これは、スカラー場\(f(x,y,z)\)の変化率を意味している。
ここで、
$$\nabla = \displaystyle\frac{\partial }{\partial x}\mathbf{i} + \displaystyle\frac{\partial }{\partial y}\mathbf{j} + \displaystyle\frac{\partial }{\partial z}\mathbf{k}\tag{2}$$
とすると、式(1)は次式のように表せる。
$$\mathrm{grad} f = \displaystyle\nabla f\tag{3}$$
(ベクトル場の)発散
ベクトル場\(\mathbf{F}(x,y,z) = F_1\mathbf{i} + F_2\mathbf{j} + F_3\mathbf{k}\)において、次のようなスカラーを「発散」という。
$$\mathrm{div} \mathbf{F} = \displaystyle\frac{\partial F_1}{\partial x} + \displaystyle\frac{\partial F_2}{\partial y} + \displaystyle\frac{\partial F_3}{\partial z}\tag{4}$$
これは、空間への物や状態の流出入を意味している。
ここで、式(2)を用いると次式のように表せる。
$$\mathrm{div} \mathbf{F} = \displaystyle\nabla \cdot \mathbf{F} \tag{5}$$
スカラー場の勾配は、方向と大きさのあるベクトル場であったが、ベクトル場の発散は、方向を持たない大きさのみのスカラー場であることに注意すれば、それぞれの物理的な意味も少しは理解しやすくなるかもしれない。
(ベクトル場の)回転
ベクトル場\(\mathbf{F}(x,y,z)\)において、次のようなベクトルを「回転」という。
\begin{equation*}
\begin{aligned}
\mathrm{rot} \, \mathbf{F}
&= \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\displaystyle\frac{\partial }{\partial x} & \displaystyle\frac{\partial }{\partial y} & \displaystyle\frac{\partial }{\partial z} \\
F_1 & F_2 & F_3
\end{vmatrix} \\
&= \left(\displaystyle\frac{\partial F_3}{\partial y} – \displaystyle\frac{\partial F_2}{\partial z}\right)\mathbf{i} + \left(\displaystyle\frac{\partial F_1}{\partial z} – \displaystyle\frac{\partial F_3}{\partial x}\right)\mathbf{j} + \left(\displaystyle\frac{\partial F_2}{\partial x} – \displaystyle\frac{\partial F_1}{\partial y}\right)\mathbf{k}
\end{aligned}
\tag{6}
\end{equation*}
これは、回転という名前の通り、現象の回転を意味している。
ここで、式(2)を用いると次式のように表せる。
$$\mathrm{rot} \mathbf{F} = \displaystyle\nabla \times \mathbf{F} \tag{7}$$
式(7)から分かるようにベクトル場の回転は、ベクトルの外積から求めることができる。ベクトルの外積の結果は、2つのベクトルが成す平行四辺形の面積と法線方向を意味している。つまり、ベクトル場の回転の物理的な意味は、回転方向と回転の大きさを表していることになる。
-場の積分
場の微分について考えた後は、もちろん場の積分についても考えていく。
現象の変化を調べるのが場の微分だとするならば、場における総量を求めるのが場の積分である。
線積分
空間の内部に点\(P\)をとり、この点\(P\)の座標は媒介変数\(t\)の関数とする。この時、\(t\)の変化に伴って点\(P\)は曲線を描く。
その曲線上の位置ベクトル\(\mathbf{r}\)は、次式のように表せる。
$$\mathbf{r} (t) = x(t) \mathbf{i} + y(t) \mathbf{j} + z(t) \mathbf{k} \tag{8}$$
また、点\(P\)の描く曲線の長さは、
$$S = \displaystyle \int_{t_0}^{t_1} \sqrt{\left(\frac{dx(t)}{dt}\right)^2+\left(\frac{dy(t)}{dt}\right)^2+\left(\frac{dz(t)}{dt}\right)^2}dt \tag{9}$$
式(9)の被積分関数は、曲線\(S\)を細かく分割した時の線の長さを意味している。このような細かくした線分を線素という。つまり、式(9)の物理的な意味は、すべての線素の長さを足し合わせたものである。
次に、場所\(\mathbf{r}\)によって値が変わるスカラー場\(f(\mathbf{r})\)を考える。
この\(f\)における線積分を考える。
$$\displaystyle \int_{t_0}^{t_1} f(\mathbf{r}) ds = \displaystyle \int_{t_0}^{t_1} f(\mathbf{r}) \sqrt{\left(\frac{dx(t)}{dt}\right)^2+\left(\frac{dy(t)}{dt}\right)^2+\left(\frac{dz(t)}{dt}\right)^2}dt \tag{10}$$
$$\displaystyle \int_{t_0}^{t_1} f(\mathbf{r}) d\mathbf{r} = \displaystyle \mathbf{i}\int_{t_0}^{t_1} f(\mathbf{r}(t))dx + \mathbf{j}\int_{t_0}^{t_1} f(\mathbf{r}(t))dy + \mathbf{k}\int_{t_0}^{t_1} f(\mathbf{r}(t))dz \tag{11}$$
式(10)は曲線\(S\)におけるスカラーの総量を意味しており、式(11)は曲線\(S\)における各成分の総量を意味している。つまり、次式で関係付けることができる。
\begin{equation*} \begin{aligned}
ds &= \left|d\mathbf{r} \right| = \displaystyle \left| \frac{d\mathbf{r}}{dt} \right| dt\\
&= \sqrt{\left(\frac{dx(t)}{dt}\right)^2+\left(\frac{dy(t)}{dt}\right)^2+\left(\frac{dz(t)}{dt}\right)^2} dt
\end{aligned} \tag{12} \end{equation*}
さらに、ベクトル場\(\mathbf{F}(\mathbf{r})\)における線積分を考える。
\begin{equation*} \begin{aligned}
\displaystyle \int_{t_0}^{t_1} \mathbf{F}(\mathbf{r}) ds &= \displaystyle \mathbf{i} \int_{t_0}^{t_1} F_1 \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2}dt\\
&+ \displaystyle \mathbf{j} \int_{t_0}^{t_1} F_2 \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2}dt\\
&+ \displaystyle \mathbf{k} \int_{t_0}^{t_1} F_3 \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2}dt
\end{aligned} \tag{13} \end{equation*}
$$\displaystyle \int_{t_0}^{t_1} \mathbf{F} \cdot d\mathbf{r} = \displaystyle \int_{t_0}^{t_1} F_1dx + \int_{t_0}^{t_1} F_2dy + \int_{t_0}^{t_1} F_3dz \tag{14}$$
ただし、\(\mathbf{F}(\mathbf{r}) = F_1\mathbf{i} + F_2\mathbf{j} + F_3\mathbf{k}\)
式(13)はベクトル場にスカラー量を乗じているので求められる量はベクトル量であり、式(14)はベクトル場とベクトル量の内積であるので求められる量はスカラー量である。
面積分
曲面\(S\)について考える。この曲面上の点\(P\)位置ベクトル\(\mathbf{r}\)を2つの媒介変数を持った関数とする。したがって、次式のように表す。
$$\mathbf{r} (u, v) = x (u, v)\mathbf{i}+ y (u, v)\mathbf{j} + z (u, v)\mathbf{k} \tag{15}$$
\(v\)を一定にして\(u\)を動かす時に曲面\(S\)に描かれる\(u\)曲線と\(u\)を一定にして\(v\)を動かす時に曲面\(S\)に描かれる\(v\)曲線の接線ベクトルはそれぞれ、\(\partial \mathbf{r}/\partial u\)と\(\partial \mathbf{r}/\partial v\)で与えられる。点\(P\)の単位法線ベクトルは次式となる。
$$\mathbf{n} = \displaystyle \frac{\displaystyle\frac{\partial \mathbf{r}}{\partial u}\times\frac{\partial \mathbf{r}}{\partial v}}{\left|\displaystyle\frac{\partial \mathbf{r}}{\partial u}\times\frac{\partial \mathbf{r}}{\partial v}\right|} \tag{16}$$
\(u\)曲線と\(v\)曲線の線素を2辺に持つ平行四辺形の面積\(dS\)は、次式のように与えられる。
$$dS = \left|\frac{\partial \mathbf{r}}{\partial u}du\times\frac{\partial \mathbf{r}}{\partial v}dv\right| = \left|\frac{\partial \mathbf{r}}{\partial u}\times\frac{\partial \mathbf{r}}{\partial v}\right|dudv \tag{17}$$
この微小面積\(dS\)を用いて、曲面の面積\(S\)を求める。
$$S = \displaystyle \int\int dS = \int\int_D \left|\frac{\partial \mathbf{r}}{\partial u}\times\frac{\partial \mathbf{r}}{\partial v}\right|dudv \tag{18}$$
式(18)を用いて曲面\(S\)に対して、スカラー場とベクトル場の面積分を定義する。
●スカラー場\(f(\mathbf{r})\)の面積分
$$\displaystyle \int_S f(\mathbf{r})dS = \int\int_D f(\mathbf{r}) \left|\frac{\partial \mathbf{r}}{\partial u}\times\frac{\partial \mathbf{r}}{\partial v}\right|dudv \tag{19}$$
●ベクトル場\(\mathbf{F}(\mathbf{r})\)の面積分
$$\displaystyle \int_S \mathbf{F}(\mathbf{r})\cdot d\mathbf{S} = \int\int_D \mathbf{F}(\mathbf{r}) \cdot \left(\frac{\partial \mathbf{r}}{\partial u}\times\frac{\partial \mathbf{r}}{\partial v}\right)dudv \tag{19}$$
ガウスの発散定理
ベクトル解析の花形である、積分公式について解説していく。積分公式で最も有名で非常に重要な定理である「ガウスの発散定理」と「ストークスの定理」について順に説明する。ここでは、各定理の証明は割愛し、物理的な意味に焦点を絞って解説していく。
まず初めに、「ガウスの発散定理」について解説する。
この「ガウスの発散定理」を簡単に説明すると、面積分と体積積分の関係式である。もう少し噛み砕くと、面積分を体積積分に変換するためによく使われる定理である。
閉曲面\(S\)に囲まれた立体\(V\)に対して、「ガウスの発散定理」は次式である。
●スカラー場
$$\displaystyle \int_S f d\mathbf{S} = \int_V \nabla f dV \tag{20}$$
●ベクトル場
$$\displaystyle \int_S \mathbf{F} \cdot d\mathbf{S} = \int_V \nabla \cdot \mathbf{F} dV \tag{21}$$
式(20)と式(21)の物理的な意味は、「立体表面から外に出ていく量= 立体内部から湧き出る量」である。
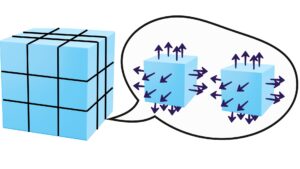
このような図でガウスの発散定理について、詳しく見てみる。
まずは、式(21)の右辺の被積分関数は、ベクトル場における発散を意味している。ベクトル場の発散とは、立体に流出入する量を表していることは前節で述べた。つまり、上図のような立体を考えた場合、式(21)の右辺は微小体積の流出入する量の合計であると言える。
この微小体積の各表面からの流出入量を考える。並んだ微小体積の向き合っている表面では、同じ大きさで逆向きの流出入量であることが直感的にわかるだろう。したがって、その表面同士は打ち消しあってゼロとなる。これを全ての微小体積に適用すると、立体\(V\)の表面積の流出入量のみの値が求められる。
ストークスの定理
次に「ストークスの定理」について解説していく。
この「ストークスの定理」は考え方は「ガウスの発散定理」と似ている。「ガウスの発散定理」は面積分と体積積分の関係式であったのに対して、「ストークスの定理」は線積分と面積分の関係式である。つまり、線積分を面積分に変換するときによく使われる定理である。
閉曲線\(C\)に囲まれた曲面\(S\)に対して、「ストークスの定理」は次式である。
$$\displaystyle \int_S (\nabla \times \mathbf{F}) \cdot d\mathbf{S} = \int_C \mathbf{F} \cdot d\mathbf{r}\tag{22}$$
式(22)の物理的な意味は、「曲面内の回転量 = 曲面境界に沿った量」である。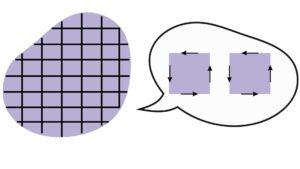
ガウスの発散定理と同様に、ストークスの定理についてもこのような図で解説すると、
まずは、式(22)の左辺の被積分関数は、ベクトル場における回転を意味している。ベクトル場の回転とは、回転方向と回転の大きさを表していることは前節で述べた。つまり、上図のような曲面を考えた場合、式(22)の左辺は微小面積の回転量の合計であると言える。
この微小面積内の回転を考える。並んだ微小面積の向き合っている境界線では、同じ大きさで逆向きの回転量であることが直感的にわかるだろう。したがって、その境界線同士は打ち消しあってゼロとなる。これを全ての微小面積に適用すると、曲面\(S\)の境界線の回転量のみの値が求められる。
これら2つの積分公式は、固体力学では頻繁に使用されている。
例えば、表面力と体積力、ひずみエネルギーの釣り合い方程式を解く際に、体積分と面積分が入り混じっていると扱いにくい。このような時に、ガウスの発散定理を用いて、面積分を体積分に変換するのだ。
ベクトルの座標変換
最後にベクトルの座標変換について解説していく。
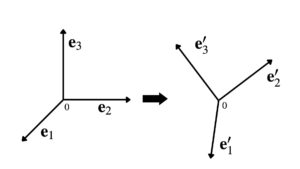
ベクトルの座標変換とは、下図のような直交座標系で定義されたベクトルに対して、原点を固定して座標軸を変化させた直行座標系でベクトルを表現し直す方法のことである。
この2つの直交座標系の基本ベクトルを\({\mathbf{e}_1 , \mathbf{e}_2 , \mathbf{e}_3}\)および\({\mathbf{e}’_1 , \mathbf{e}’_2 , \mathbf{e}’_3}\)とすると、次式のような関係が成り立つとする。
$$\left.\begin{align}
\mathbf{e}_1 &= \beta_{11}\mathbf{e}’_1 + \beta_{21}\mathbf{e}’_2 + \beta_{31}\mathbf{e}’_3 \\
\mathbf{e}_2 &= \beta_{12}\mathbf{e}’_1 + \beta_{22}\mathbf{e}’_2 + \beta_{32}\mathbf{e}’_3 \\
\mathbf{e}_3 &= \beta_{13}\mathbf{e}’_1 + \beta_{23}\mathbf{e}’_2 + \beta_{33}\mathbf{e}’_3
\end{align}\right\} \tag{23}$$
この時、\(\mathbf{e}’\)の直行性から\(\beta_{ij} = \mathbf{e}’_i \cdot \mathbf{e}_j\)となる。
次に、任意の位置ベクトル\(\mathbf{a}\)を基本ベクトルの線形和で表現すれば、
\begin{equation*} \begin{aligned}
\mathbf{a} &= a_1\mathbf{e}_1 + a_2\mathbf{e}_2 + a_3\mathbf{e}_3\\
&= a’_1\mathbf{e}’_1 + a’_2\mathbf{e}’_2 + a’_3\mathbf{e}’_3
\end{aligned} \tag{24} \end{equation*}
と書くことができる。式(23)を式(24)に代入すれば、
\begin{equation*} \begin{aligned}
a’_1\mathbf{e}’_1 + a’_2\mathbf{e}’_2 + a’_3\mathbf{e}’_3
=& (\beta_{11}a_1 + \beta_{12}a_2 + \beta_{13}a_3) \mathbf{e}’_1\\
&+ (\beta_{22}a_1 + \beta_{22}a_2 + \beta_{23}a_3) \mathbf{e}’_2\\
&+ (\beta_{31}a_1 + \beta_{32}a_2 + \beta_{33}a_3) \mathbf{e}’_3
\end{aligned} \tag{25} \end{equation*}
式(25)の\(\mathbf{e}’_1 , \mathbf{e}’_2 , \mathbf{e}’_3\)の係数を比較すると、
\begin{equation*}
\left[\begin{array}{c}
a’_{1} \\
a’_{2} \\
a’_{3} \\
\end{array}\right]
=
\left[ \begin{array}{ccc}
\beta_{11} & \beta_{12} & \beta_{13} \\
\beta_{21} & \beta_{22} & \beta_{23} \\
\beta_{31} & \beta_{32} & \beta_{33} \\
\end{array}\right]
\left[ \begin{array}{c}
a_1 \\
a_2 \\
a_3 \\
\end{array}\right]
\tag{26}
\end{equation*}
式(26)右辺の\(3 \times 3\)の行列を座標変換行列という。

