四角形1次要素を用いて2次元応力解析をするためのPythonコードを載せておく。
CAEとFEMとは?~構造解析の計算の流れ~ を基に作成した。
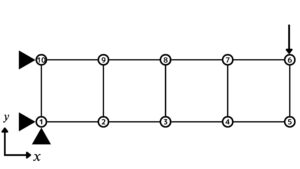
応力解析をするためのPythonコードを作成するにあたって、下図のような4要素で構成された簡単な解析モデルを題材にした。
各節点間の距離は1[mm]とし、固定支持した梁の端点に荷重を100[N]与えている。
要素の物性値は、ヤング率210000[MPa]、ポアソン比0.3[-]の鋼材を想定している。
構造解析をする上で最も重要なポイントが、単位系である。単位系とは、[N]や[MPa]などのような数値の物理的な意味のことである。構造解析のアルゴリズム内では、単位系は一切考慮されず、数値のみを操作している。そのため、入力する値の単位が揃っていないと、全く異なる結果が得られえることになる。
import math
root3 = math.sqrt(3)
nodes = 10 #全節点数
elements = 4 #全要素数
thickness = 0.01 #要素の厚さ
young = 210000 #ヤング率
poisson = 0.3 #ポアソン比
components = 3 #ひずみと応力の成分数
nodes_quad4 = 4 #四角形1次要素の節点数
integral_points = 4 #要素の積分点数
dof_node = 2 #節点自由度
dof_total = dof_node * nodes #全自由度
dof_quad4 = dof_node * nodes_quad4 #要素自由度
#積分点座標、重み
ip_xi = [0.0 for _ in range(integral_points)]
ip_et = [0.0 for _ in range(integral_points)]
ip_wi = [0.0 for _ in range(integral_points)]
ip_wj = [0.0 for _ in range(integral_points)]
#節点のX座標配列
x = [0.0 for _ in range(nodes)]
#節点のY座標配列
y = [0.0 for _ in range(nodes)]
#要素内節点順配列
connectivity = [[0.0 for _ in range(nodes_quad4)] for _ in range(elements)]
#Dマトリクス
D = [[0.0 for _ in range(components)] for _ in range(components)]
#Bマトリクス
B = [[[[0.0 for _ in range(dof_quad4)] for _ in range(components)] for _ in range(integral_points)] for _ in range(elements)]
#ヤコビ行列
detJ = [[0.0 for _ in range(integral_points)] for _ in range(elements)]
#要素剛性マトリクスの配列
Ke = [[[0.0 for _ in range(dof_quad4)] for _ in range(dof_quad4)] for _ in range(elements)]
#全体剛性マトリクスの配列
K = [[0.0 for _ in range(dof_total)] for _ in range(dof_total)]
#計算用全体剛性マトリクスの配列
Kc = [[0.0 for _ in range(dof_total)] for _ in range(dof_total)]
#境界条件ベクトルの配列
U = [0.0 for _ in range(dof_total)]
F = [0.0 for _ in range(dof_total)]
Um = [0.0 for _ in range(dof_total)]
#反力ベクトル
Fr = [0.0 for _ in range(dof_total)]
#積分点ひずみ
strain_ip = [[[0.0 for _ in range(components)] for _ in range(integral_points)] for _ in range(elements)]
#積分点応力
stress_ip = [[[0.0 for _ in range(components)] for _ in range(integral_points)] for _ in range(elements)]
def main():
initialize()
make_D()
make_B()
make_Ke()
make_K()
set_boundary_condition()
solve()
make_reaction()
make_strain_element()
make_stress_element()
for e in range(0,elements):
for ip in range(0,integral_points):
for r in range(0,components):
print(stress_ip[e][ip][r])
def initialize():
#要素内節点順を設定
connectivity[0][0] = 1
connectivity[0][1] = 2
connectivity[0][2] = 9
connectivity[0][3] = 10
connectivity[1][0] = 2
connectivity[1][1] = 3
connectivity[1][2] = 8
connectivity[1][3] = 9
connectivity[2][0] = 3
connectivity[2][1] = 4
connectivity[2][2] = 7
connectivity[2][3] = 8
connectivity[3][0] = 4
connectivity[3][1] = 5
connectivity[3][2] = 6
connectivity[3][3] = 7
#節点座標配列を設定
x[0] = 0.0
x[1] = 1.0
x[2] = 2.0
x[3] = 3.0
x[4] = 4.0
x[5] = 4.0
x[6] = 3.0
x[7] = 2.0
x[8] = 1.0
x[9] = 0.0
y[0] = 0.0
y[1] = 0.0
y[2] = 0.0
y[3] = 0.0
y[4] = 0.0
y[5] = 1.0
y[6] = 1.0
y[7] = 1.0
y[8] = 1.0
y[9] = 1.0
#変位ベクトルを設定
U[0] = 0.0
U[1] = 0.0
U[2] = 0.0
U[3] = 0.0
U[4] = 0.0
U[5] = 0.0
U[6] = 0.0
U[7] = 0.0
U[8] = 0.0
U[9] = 0.0
U[10] = 0.0
U[11] = 0.0
U[12] = 0.0
U[13] = 0.0
U[14] = 0.0
U[15] = 0.0
U[16] = 0.0
U[17] = 0.0
U[18] = 0.0
U[19] = 0.0
#荷重ベクトルを設定
F[0] = 0.0
F[1] = 0.0
F[2] = 0.0
F[3] = 0.0
F[4] = 0.0
F[5] = 0.0
F[6] = 0.0
F[7] = 0.0
F[8] = 0.0
F[9] = 0.0
F[10] = 0.0
F[11] = -100.0
F[12] = 0.0
F[13] = 0.0
F[14] = 0.0
F[15] = 0.0
F[16] = 0.0
F[17] = 0.0
F[18] = 0.0
F[19] = 0.0
#拘束目印ベクトルを設定
Um[0] = True
Um[1] = True
Um[2] = False
Um[3] = False
Um[4] = False
Um[5] = False
Um[6] = False
Um[7] = False
Um[8] = False
Um[9] = False
Um[10] = False
Um[11] = False
Um[12] = False
Um[13] = False
Um[14] = False
Um[15] = False
Um[16] = False
Um[17] = False
Um[18] = True
Um[19] = False
#積分点座標
ip_xi[0] = - 1 / root3
ip_xi[1] = 1 / root3
ip_xi[2] = - 1 / root3
ip_xi[3] = 1 / root3
ip_et[0] = - 1 / root3
ip_et[1] = - 1 / root3
ip_et[2] = 1 / root3
ip_et[3] = 1 / root3
#積分点重み
ip_wi[0] = 1.0
ip_wi[1] = 1.0
ip_wi[2] = 1.0
ip_wi[3] = 1.0
ip_wj[0] = 1.0
ip_wj[1] = 1.0
ip_wj[2] = 1.0
ip_wj[3] = 1.0
def make_D():
coef = young / (1.0 - 2.0 * poisson) / (1.0 + poisson)
D[0][0] = coef * (1.0 - poisson)
D[0][1] = coef * poisson
D[0][2] = 0.0
D[1][0] = D[0][1]
D[1][1] = coef * (1.0 - poisson)
D[1][2] = 0.0
D[2][0] = D[0][2]
D[2][1] = D[1][2]
D[2][2] = coef * (1.0 - 2.0 * poisson) / 2.0
def make_B():
for e in range(0,elements):
x1 = x[connectivity[e][0]-1]
x2 = x[connectivity[e][1]-1]
x3 = x[connectivity[e][2]-1]
x4 = x[connectivity[e][3]-1]
y1 = y[connectivity[e][0]-1]
y2 = y[connectivity[e][1]-1]
y3 = y[connectivity[e][2]-1]
y4 = y[connectivity[e][3]-1]
for ip in range(0,integral_points):
xi = ip_xi[ip]
et = ip_et[ip]
dN1dXi = - (1 - et) / 4
dN2dXi = (1 - et) / 4
dN3dXi = (1 + et) / 4
dN4dXi = - (1 + et) / 4
dN1dEt = - (1 - xi) / 4
dN2dEt = - (1 + xi) / 4
dN3dEt = (1 + xi) / 4
dN4dEt = (1 - xi) / 4
dXdXi = dN1dXi*x1 + dN2dXi*x2 + dN3dXi*x3 + dN4dXi*x4
dXdEt = dN1dEt*x1 + dN2dEt*x2 + dN3dEt*x3 + dN4dEt*x4
dYdXi = dN1dXi*y1 + dN2dXi*y2 + dN3dXi*y3 + dN4dXi*y4
dYdEt = dN1dEt*x1 + dN2dEt*x2 + dN3dEt*x3 + dN4dEt*x4
detJ[e][ip] = dXdXi * dYdEt - dXdEt * dYdXi
dN1dX = (dN1dXi * dYdEt - dN1dEt * dYdXi) / detJ[e][ip]
dN2dX = (dN2dXi * dYdEt - dN2dEt * dYdXi) / detJ[e][ip]
dN3dX = (dN3dXi * dYdEt - dN3dEt * dYdXi) / detJ[e][ip]
dN4dX = (dN4dXi * dYdEt - dN4dEt * dYdXi) / detJ[e][ip]
dN1dY = ( - dN1dXi * dXdEt + dN1dEt * dXdXi) / detJ[e][ip]
dN2dY = ( - dN2dXi * dXdEt + dN2dEt * dXdXi) / detJ[e][ip]
dN3dY = ( - dN3dXi * dXdEt + dN3dEt * dXdXi) / detJ[e][ip]
dN4dY = ( - dN4dXi * dXdEt + dN4dEt * dXdXi) / detJ[e][ip]
B[e][ip][0][0] = dN1dX
B[e][ip][0][1] = 0.0
B[e][ip][0][2] = dN2dX
B[e][ip][0][3] = 0.0
B[e][ip][0][4] = dN3dX
B[e][ip][0][5] = 0.0
B[e][ip][0][6] = dN4dX
B[e][ip][0][7] = 0.0
B[e][ip][1][0] = 0.0
B[e][ip][1][1] = dN1dY
B[e][ip][1][2] = 0.0
B[e][ip][1][3] = dN2dY
B[e][ip][1][4] = 0.0
B[e][ip][1][5] = dN3dY
B[e][ip][1][6] = 0.0
B[e][ip][1][7] = dN3dY
B[e][ip][2][0] = dN1dY
B[e][ip][2][1] = dN1dX
B[e][ip][2][2] = dN2dY
B[e][ip][2][3] = dN2dX
B[e][ip][2][4] = dN3dY
B[e][ip][2][5] = dN3dX
B[e][ip][2][6] = dN4dY
B[e][ip][2][7] = dN4dX
def make_Ke():
Dt = [[0.0 for _ in range(components)] for _ in range(components)]
Bt = [[0.0 for _ in range(components)] for _ in range(dof_quad4)]
BtDt = [[0.0 for _ in range(components)] for _ in range(dof_quad4)]
#Dマトリクスの転置
for r in range(0,components):
for c in range(0,components):
Dt[c][r] = D[r][c]
for e in range(0,elements):
#Bマトリクスの転置
for ip in range(0,integral_points):
for r in range(0,components):
for c in range(0,dof_quad4):
Bt[c][r] = B[e][ip][r][c]
#Bt✖️Dtの計算
for r in range(0,dof_quad4):
for c in range(0,components):
BtDt[r][c] = 0.0
for m in range(0,components):
BtDt[r][c] = BtDt[r][c] + Bt[r][m] * Dt[m][c]
#積分点剛性マトリクスKepの計算
Kep = [[0.0 for _ in range(dof_quad4)] for _ in range(dof_quad4)]
for r in range(0,dof_quad4):
for c in range(0,dof_quad4):
Kep[r][c] = 0.0
for m in range(0,components):
Kep[r][c] = Kep[r][c] + BtDt[r][m] * B[e][ip][m][c]
wi = ip_wi[ip]
wj = ip_wj[ip]
Kep[r][c] = Kep[r][c] * detJ[e][ip] * wi * wj * thickness
#要素剛性マトリクスKeの計算
for r in range(0,components):
for c in range(0,components):
Ke[e][r][c] = Ke[e][r][c] + Kep[r][c]
def make_K():
for rt in range(0,dof_total):
for ct in range(0,dof_total):
K[rt][ct] = 0.0
for e in range(0,elements):
for r in range(0,dof_quad4):
rt = (connectivity[e][r // dof_node] * dof_node - ((r+1) % dof_node)) - 1
for c in range(0,dof_quad4):
ct = (connectivity[e][c // dof_node] * dof_node - ((c+1) % dof_node)) -1
K[rt][ct] = K[rt][ct] + Ke[e][r][c]
def set_boundary_condition():
for r in range(0,dof_total):
for c in range(0,dof_total):
Kc[r][c] = K[r][c]
for r in range(0,dof_total):
if Um[r] == True:
for rr in range(0,dof_total):
if rr != r:
F[rr] = F[rr] - Kc[rr][r] * U[r]
for rr in range(0,dof_total):
Kc[rr][r] = 0.0
for cc in range(0,dof_total):
Kc[r][cc] = 0.0
Kc[r][r] = 1.0
F[r] = U[r]
def solve():
pivot = 0
p = 0
for r in range(0,dof_total):
pivot = Kc[r][r]
for c in range(r,dof_total):
Kc[r][c] = Kc[r][c] / pivot
F[r] = F[r] / pivot
for rr in range(r+1, dof_total):
p = Kc[rr][r]
for cc in range(r,dof_total):
Kc[rr][cc] = Kc[rr][cc] - p * Kc[r][cc]
F[rr] = F[rr] - p * F[r]
for r in range(dof_total-1,-1,-1):
U[r] = F[r]
if r != dof_total-1:
for c in range(r+1,dof_total):
U[r] = U[r] - Kc[r][c] * U[c]
def make_reaction():
for r in range(dof_total):
Fr[r] = 0.0
for c in range(0,dof_total):
Fr[r] = Fr[r] + K[r][c] * U[c]
def make_strain_element():
Ue = [0.0 for _ in range(dof_quad4)]
for e in range(0,elements):
for ip in range(0,integral_points):
for n in range(0,nodes_quad4):
Ue[n * 2] = U[connectivity[e][n] * 2 - 2]
Ue[n * 2 + 1] = U[connectivity[e][n] * 2 - 1]
for r in range(0,components):
strain_ip[e][ip][r] = 0
for c in range(0,dof_quad4):
strain_ip[e][ip][r] = strain_ip[e][ip][r] + B[e][ip][r][c] * Ue[c]
def make_stress_element():
for e in range(0,elements):
for ip in range(0,integral_points):
for r in range(0,components):
stress_ip[e][ip][r] = 0
for c in range(0,components):
stress_ip[e][ip][r] = stress_ip[e][ip][r] + D[r][c] * strain_ip[e][ip][c]
main()

