-要素の役割
構造物全体の挙動を1つの関数で表現するのは非常に困難である。そこで、FEMでは、構造物の挙動を要素と呼ぶ単純な形状に分割し、その要素内では変位分布を単純な関数で表現して、全体の挙動を表現しようと考える。近似の精度を高めたい場合には、分割を細かくしていけば良い。分割した要素内の変位分布を表現した関数を「変位関数」と呼ぶ。
例えば簡単な1次元の関数で変位関数を解説する。下の左図に示すような直線上の区間\(a \leq x \leq b\)で、1方向にだけ変位分布\(\delta = f(x)\)が発生しているとする。つまり、梁の変位を表した関数である。この変位分布を右図のように折れ線(1次関数)近似したとすると、それぞれの線分が要素である。線分を表示する式は、係数2個を使って次式のように表すことができる。このような式が変位関数である。
$$\delta = c_1 + c_2x$$
ただし、\(c_1\)、\(c_2\)は未定係数である。未定係数は、小区間の両端の\(x\)座標によって決定される。
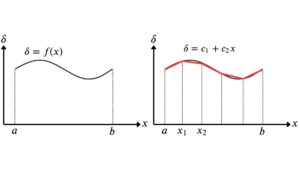
もし小区間を1次関数ではなく2次関数で近似しようとすれば、小区間の両端と区間内にもう1点(計3点)取ることによって、変位関数は次式で表される。
$$\delta = c_1 + c_2x + c_3x^2$$
この変位関数を考える上で注意点として、変位関数の未定係数と小区間内に必要な点(節点数)は、同じ数でなければならない。
さらに、変位関数は、要素節点数と未知数が一致していれば良いというものではなく、下記のようないくつかの制約条件が課される。
① 剛体変位と剛体回転に対して、ひずみが発生しない。
② 一定ひずみの状態が表現できること
③ 隣合う要素の境界辺(面)上の変位は、その辺(面)上のすべての点で等しいこと。
④ シェル要素では、隣合う要素の境界辺(面)上の回転は、その辺(面)上の全ての点で等しいこと。
-三角形1次要素
変位関数の概要を理解できたところで、次は2次元の要素について解説していく。有限要素法で最も注意するべきポイントが、解析対象の構造物をどの要素で分割するかである。そこで重要になってくる概念が、「形状関数」と「\(B\)マトリクス」である。
形状関数
三角形1次要素は、変位関数が下式になるような2次元問題用の要素である。
$$\left.\array{\delta_x=&c_1 + c_2x + c_3y\\\delta_y=&d_1 + d_2x + d_3y}\right\} \tag{1}$$
式(1)は、要素内の任意の点における変位は、その点の座標の1次関数で表現できることを意味する。式(1)の\(c_1\)~\(c_3\)と\(d_1\)~\(d_3\)を求めることで、要素内の変位を算出する。
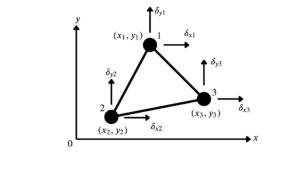
まずは、節点1,2,3における節点変位\(\left(\delta_{x1},\delta_{y1}\right)\),\(\left(\delta_{x2},\delta_{y2}\right)\),\(\left(\delta_{x3},\delta_{y3}\right)\)は、式(1)を満たすことから節点変位と節点座標を式(1)に代入すると、次式ができる。
\begin{equation*}
\left\{
\begin{array}{c}
\delta_{x1} \\
\delta_{x2} \\
\delta_{x3}
\end{array}
\right\}=
\left[
\begin{array}{cccccc}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{array}
\right]
\left\{
\begin{array}{c}
c_1 \\
c_2 \\
c_3
\end{array}
\right\}
\tag{2}\end{equation*}
\begin{equation*}
\left\{
\begin{array}{c}
\delta_{y1} \\
\delta_{y2} \\
\delta_{y3}
\end{array}
\right\}=
\left[
\begin{array}{cccccc}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{array}
\right]
\left\{
\begin{array}{c}
d_1 \\
d_2 \\
d_3
\end{array}
\right\}
\tag{3}\end{equation*}
式(2),(3)を解いて、\(c_1\)~\(c_3\)と\(d_1\)~\(d_3\)を求める。
$$\left.\array{c_1 =& \displaystyle\frac{\left(y_2-y_3\right)\delta_{x1} + \left(y_3-y_3\right)\delta_{x2} + \left(y_1-y_2\right)\delta_{x3}}{x_1y_2 + x_2y_3 + x_3y_1 – x_1y_3 – x_2y_1 – x_3y_2}\\
c_2 =& \displaystyle\frac{\left(x_3-x_2\right)\delta_{x1} + \left(x_1-x_3\right)\delta_{x2} + \left(x_2-x_1\right)\delta_{x3}}{x_1y_2 + x_2y_3 + x_3y_1 – x_1y_3 – x_2y_1 – x_3y_2}\\
c_3 =& \displaystyle\frac{\left(x_2y_3 – x_3y_2\right)\delta_{x1} + \left(x_3y_1 – x_1y_3\right)\delta_{x2} + \left(x_1y_2 – x_2y_1\right)\delta_{x3}}{x_1y_2 + x_2y_3 + x_3y_1 – x_1y_3 – x_2y_1 – x_3y_2}\\
d_1 =& \displaystyle\frac{\left(y_2-y_3\right)\delta_{y1} + \left(y_3-y_3\right)\delta_{y2} + \left(y_1-y_2\right)\delta_{y3}}{x_1y_2 + x_2y_3 + x_3y_1 – x_1y_3 – x_2y_1 – x_3y_2}\\
d_2 =& \displaystyle\frac{\left(x_3-x_2\right)\delta_{y1} + \left(x_1-x_3\right)\delta_{y2} + \left(x_2-x_1\right)\delta_{y3}}{x_1y_2 + x_2y_3 + x_3y_1 – x_1y_3 – x_2y_1 – x_3y_2}\\
d_3 =& \displaystyle\frac{\left(x_2y_3 – x_3y_2\right)\delta_{y1} + \left(x_3y_1 – x_1y_3\right)\delta_{y2} + \left(x_1y_2 – x_2y_1\right)\delta_{y3}}{x_1y_2 + x_2y_3 + x_3y_1 – x_1y_3 – x_2y_1 – x_3y_2}}\right\} \tag{4}$$
式(4)の分母は全て同じであり、三角形要素の面積の2倍である。したがって、これを次式のように表すことにする。
$$2\Delta = x_1y_2 + x_2y_3 + x_3y_1 – x_1y_3 – x_2y_1 – x_3y_2$$
式(4)を式(1)に代入して、\(\delta_{x_1}\),\(\delta_{x_2}\),\(\delta_{x_3}\),\(\delta_{y_1}\),\(\delta_{y2}\),\(\delta_{y3}\)でまとめると、要素内部の任意の点の変位\(\left(\delta_x,\delta_y\right)\)をその点の座標\(\left(x,y\right)\)と節点の座標\(\left(x_1,y_1\right)\),\(\left(x_2,y_2\right)\),\(\left(x_3,y_3\right)\)および節点の変位\(\left(\delta_{x1},\delta_{y1}\right)\),\(\left(\delta_{x2},\delta_{y2}\right)\),\(\left(\delta_{x3},\delta_{y3}\right)\)とで表現することができる。
\begin{equation*}
\delta_x = \displaystyle\frac{1}{2\Delta} \left[ \begin{array}{c}
\left\{ (y_2 – y_3)x + (x_3 – x_2)y + (x_2y_3 – x_3y_2) \right\}\delta_{x1} \\
+ \left\{ (y_3 – y_1)x + (x_1 – x_3)y + (x_3y_1 – x_1y_3) \right\}\delta_{x2} \\
+ \left\{ (y_1 – y_2)x + (x_2 – x_1)y + (x_1y_2 – x_2y_1) \right\}\delta_{x3}
\end{array} \right]
\tag{5}\end{equation*}
\begin{equation*}
\delta_y = \displaystyle\frac{1}{2\Delta} \left[ \begin{array}{c}
\left\{ (y_2 – y_3)x + (x_3 – x_2)y + (x_2y_3 – x_3y_2) \right\}\delta_{y1} \\
+ \left\{ (y_3 – y_1)x + (x_1 – x_3)y + (x_3y_1 – x_1y_3) \right\}\delta_{y2} \\
+ \left\{ (y_1 – y_2)x + (x_2 – x_1)y + (x_1y_2 – x_2y_1) \right\}\delta_{y3}
\end{array} \right]
\tag{6}\end{equation*}
節点の値から要素内の任意の点の値を求める式を「形状関数」という。形状関数は要素内の座標関数である。三角形1次要素の形状関数は、次式であることがわかる。
$$\left.\array{N_1\left(x,y\right) = \displaystyle\frac{1}{2\Delta}\left\{\left(y_2 – y_3\right)x + \left(x_3 – x_2\right)y + \left(x_2y_3 – x_3y_2\right)\right\}\\
N_2\left(x,y\right) = \displaystyle\frac{1}{2\Delta}\left\{\left(y_3 – y_1\right)x + \left(x_1 – x_3\right)y + \left(x_3y_1 – x_1y_3\right)\right\}\\
N_3\left(x,y\right) = \displaystyle\frac{1}{2\Delta}\left\{\left(y_1 – y_2\right)x + \left(x_2 – x_1\right)y + \left(x_1y_2 – x_2y_1\right)\right\}}\right\} \tag{7}$$
式(5)(6)に式(7)を代入して、要素内部の任意の点の変位\(\left(\delta_x,\delta_y\right)\)の式を簡潔に表現すると、
$$\delta_x = N_1\delta_{x1} + N_2\delta_{x2} + N_3\delta_{x3}\tag{8}$$
$$\delta_y = N_1\delta_{y1} + N_2\delta_{y2} + N_3\delta_{y3}\tag{9}$$
形状関数は要素内の任意の点に対する各節点の重みを表しているとも言える。
\(B\)マトリクス
節点の変位を形状関数を用いて表現できることが分かった。次に考えることは、ひずみである。
ひずみは変位の座標に関する1階微分である。変数は、要素内部の座標\(\left(x,y\right)\)であり、節点変位\(\delta_{x1}\),\(\delta_{x2}\),\(\delta_{x3}\),\(\delta_{y1}\),\(\delta_{y2}\),\(\delta_{y3}\)は定数とみなすことができる。つまり、微分の対象は形状関数だけであり、式(8)(9)を微分する。
$$\left.\array{\displaystyle\frac{\partial \delta_x}{\partial x} = \displaystyle\frac{\partial N_1}{\partial x}\delta_{x1} + \displaystyle\frac{\partial N_2}{\partial x}\delta_{x2} + \displaystyle\frac{\partial N_3}{\partial x}\delta_{x3}\\
\displaystyle\frac{\partial \delta_x}{\partial y} = \displaystyle\frac{\partial N_1}{\partial y}\delta_{x1} + \displaystyle\frac{\partial N_2}{\partial y}\delta_{x2} + \displaystyle\frac{\partial N_3}{\partial y}\delta_{x3}\\
\displaystyle\frac{\partial \delta_y}{\partial x} = \displaystyle\frac{\partial N_1}{\partial x}\delta_{y1} + \displaystyle\frac{\partial N_2}{\partial x}\delta_{y2} + \displaystyle\frac{\partial N_3}{\partial x}\delta_{y3}\\
\displaystyle\frac{\partial \delta_y}{\partial y} = \displaystyle\frac{\partial N_1}{\partial y}\delta_{y1} + \displaystyle\frac{\partial N_2}{\partial y}\delta_{y2} + \displaystyle\frac{\partial N_3}{\partial y}\delta_{y3}}\right\} \tag{10}$$
\(xy\)平面内の2次元ひずみは、\(x\)方向、\(y\)方向、\(xy\)平面内のせん断方向の3成分から構成され、次のように表される。
\begin{equation*}
\left\{
\begin{array}{c}
\epsilon
\end{array}
\right\}=
\left\{
\begin{array}{c}
\displaystyle\frac{\partial \delta_x}{\partial x} \\
\displaystyle\frac{\partial \delta_y}{\partial y} \\
\displaystyle\frac{\partial \delta_x}{\partial y} + \frac{\partial \delta_y}{\partial x}
\end{array}
\right\}
\tag{11}\end{equation*}
式(10)を式(11)に代入すると、
\begin{equation*}
\left\{
\begin{array}{c}
\epsilon
\end{array}
\right\}=
\left\{
\begin{array}{c}
\displaystyle\frac{\partial N_1}{\partial x}\delta_{x1} + \displaystyle\frac{\partial N_2}{\partial x}\delta_{x2} + \displaystyle\frac{\partial N_3}{\partial x}\delta_{x3} \\
\displaystyle\frac{\partial N_1}{\partial y}\delta_{y1} + \displaystyle\frac{\partial N_2}{\partial y}\delta_{y2} + \displaystyle\frac{\partial N_3}{\partial y}\delta_{y3} \\
\displaystyle\frac{\partial N_1}{\partial y}\delta_{x1} + \displaystyle\frac{\partial N_2}{\partial y}\delta_{x2} + \displaystyle\frac{\partial N_3}{\partial y}\delta_{x3} + \displaystyle\frac{\partial N_1}{\partial x}\delta_{y1} + \displaystyle\frac{\partial N_2}{\partial x}\delta_{y2} + \displaystyle\frac{\partial N_3}{\partial x}\delta_{y3}
\end{array}
\right\}
\end{equation*}
が得られる。行列の式で表現すると、
\begin{equation*}
\left\{
\begin{array}{c}
\epsilon
\end{array}
\right\}=
\left[
\begin{array}{cccccc}
\displaystyle\frac{\partial N_1}{\partial x} & 0 & \displaystyle\frac{\partial N_2}{\partial x} & 0 & \displaystyle\frac{\partial N_3}{\partial x} & 0 \\
0 & \displaystyle\frac{\partial N_1}{\partial y} & 0 & \displaystyle\frac{\partial N_2}{\partial y} & 0 & \displaystyle\frac{\partial N_3}{\partial y} \\
\displaystyle\frac{\partial N_1}{\partial y} & \displaystyle\frac{\partial N_1}{\partial x} & \displaystyle\frac{\partial N_2}{\partial y} & \displaystyle\frac{\partial N_2}{\partial x} & \displaystyle\frac{\partial N_3}{\partial y} & \displaystyle\frac{\partial N_3}{\partial x}
\end{array}
\right]
\left\{
\begin{array}{c}
\delta_{x1} \\
\delta_{y1} \\
\delta_{x2}\\
\delta_{y2} \\
\delta_{x3} \\
\delta_{y3}
\end{array}
\right\}
\tag{12}\end{equation*}
式(12)は、三角形1次要素の節点変位とひずみの関係を表している。右辺の行列を「\(B\)マトリクス」といい、\(\left[B\right]\)と表記する。また右辺のベクトルは、要素の節点変位ベクトル\(\left\{u\right\}\)である。
すなわち、
$$\left\{\epsilon\right\} = \left[B\right]\left\{u\right\}$$
\begin{align*}
\left[ \begin{array}{c} B \end{array} \right] &= \left[ \begin{array}{cccccc}
\displaystyle\frac{\partial N_1}{\partial x} & 0 & \displaystyle\frac{\partial N_2}{\partial x} & 0 & \displaystyle\frac{\partial N_3}{\partial x} & 0 \\
0 & \displaystyle\frac{\partial N_1}{\partial y} & 0 & \displaystyle\frac{\partial N_2}{\partial y} & 0 & \displaystyle\frac{\partial N_3}{\partial y} \\
\displaystyle\frac{\partial N_1}{\partial y} & \displaystyle\frac{\partial N_1}{\partial x} & \displaystyle\frac{\partial N_2}{\partial y} & \displaystyle\frac{\partial N_2}{\partial x} & \displaystyle\frac{\partial N_3}{\partial y} & \displaystyle\frac{\partial N_3}{\partial x}
\end{array} \right]\\
&= \displaystyle\frac{1}{2\Delta} \left[ \begin{array}{cccccc}
y_2 – y_3 & 0 & y_3 – y_1 & 0 & y_1 – y_2 & 0 \\
0 & x_3 – x_2 & 0 & x_1 – x_3 & 0 & x_2 – x_1 \\
x_3 – x_2 & y_2 – y_3 & x_1 – x_3 & y_3 – y_1 & x_2 – x_1 & y_1 – y_2
\end{array} \right]
\end{align*}
三角形1次要素の\(B\)マトリクスを見ると、要素の節点座標のみで構成されていることが分かる。つまり、要素内のひずみは、\(x,y\)座標に依らず一定であることを意味している。
-四角形1次要素
三角形1次要素の形状関数と\(B\)マトリクスは比較的容易に理解できるであろう。しかし、実際に三角形1次要素を用いて解析することは滅多にない。前述した通り、三角形1次要素は要素内のひずみが一定で計算されてしまうことが、使われない大きな理由である。
そこで、三角形1次要素よりも高精度に解析できる要素を考える。そのような要素は多数存在するが、その1つとして、四角形1次要素を解説する。
形状関数
形が任意の不等辺四角形の内部の点を考えるとき、考えやすいように座標\(\left(x,y\right)\)を\(\left(\eta,\xi\right)\)の座標系となる正方形に変換する。この座標の変換を写像という。座標\(\left(x,y\right)\)と座標\(\left(\eta,\xi\right)\)の対応関係は下式である。
$$x = \displaystyle\frac{\left(1 – \xi\right)\left(1 – \eta\right)}{4}x_1 + \displaystyle\frac{\left(1 + \xi\right)\left(1 – \eta\right)}{4}x_2 + \displaystyle\frac{\left(1 + \xi\right)\left(1 + \eta\right)}{4}x_3 + \displaystyle\frac{\left(1 – \xi\right)\left(1 + \eta\right)}{4}x_4\tag{13}$$
$$y = \displaystyle\frac{\left(1 – \xi\right)\left(1 – \eta\right)}{4}y_1 + \displaystyle\frac{\left(1 + \xi\right)\left(1 – \eta\right)}{4}y_2 + \displaystyle\frac{\left(1 + \xi\right)\left(1 + \eta\right)}{4}y_3 + \displaystyle\frac{\left(1 – \xi\right)\left(1 + \eta\right)}{4}y_4\tag{14}$$
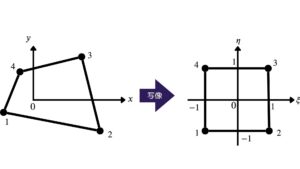 座標\(\left(x,y\right)\)と座標\(\left(\eta,\xi\right)\)の対応関係の式は、節点変位の式にも適用できる。このように、変位関数と写像関数が同じ係数関数で表される要素のことを、「アイソパラメトリック要素」と呼ぶ。
座標\(\left(x,y\right)\)と座標\(\left(\eta,\xi\right)\)の対応関係の式は、節点変位の式にも適用できる。このように、変位関数と写像関数が同じ係数関数で表される要素のことを、「アイソパラメトリック要素」と呼ぶ。
$$\delta_x = \displaystyle\frac{\left(1 – \xi\right)\left(1 – \eta\right)}{4}\delta_{x1} + \displaystyle\frac{\left(1 + \xi\right)\left(1 – \eta\right)}{4}\delta_{x2} + \displaystyle\frac{\left(1 + \xi\right)\left(1 + \eta\right)}{4}\delta_{x3} + \displaystyle\frac{\left(1 – \xi\right)\left(1 + \eta\right)}{4}\delta_{x4}\tag{15}$$
$$\delta_y = \displaystyle\frac{\left(1 – \xi\right)\left(1 – \eta\right)}{4}\delta_{y1} + \displaystyle\frac{\left(1 + \xi\right)\left(1 – \eta\right)}{4}\delta_{y2} + \displaystyle\frac{\left(1 + \xi\right)\left(1 + \eta\right)}{4}\delta_{y3} + \displaystyle\frac{\left(1 – \xi\right)\left(1 + \eta\right)}{4}\delta_{y4}\tag{16}$$
したがって、四角形1次要素の形状関数は次式となる。
$$\left.\array{N_1\left(x,y\right) = \displaystyle\frac{\left(1 – \xi\right)\left(1 – \eta\right)}{4}\\
N_2\left(x,y\right) = \displaystyle\frac{\left(1 + \xi\right)\left(1 – \eta\right)}{4}\\
N_3\left(x,y\right) = \displaystyle\frac{\left(1 + \xi\right)\left(1 + \eta\right)}{4}\\
N_4\left(x,y\right) = \displaystyle\frac{\left(1 – \xi\right)\left(1 + \eta\right)}{4}}\right\} \tag{17}$$
現在のFEMで使用されている要素の大半はアイソパラメトリック要素である。しかし、ごく一部では別のプログラムを使用している場合もあって、これは外観では判断ができないため、汎用FEMソフトのマニュアルを参照する必要がある。
\(B\)マトリクス
三角形1次要素で説明したように、\(B\)マトリクスは下式のように表される。
\begin{align}
\left[ \begin{array}{c} B \end{array} \right] &= \left[ \begin{array}{cccccc}
\displaystyle \frac{\partial N_1}{\partial x} & 0 & \displaystyle \frac{\partial N_2}{\partial x} & 0 & \displaystyle \frac{\partial N_3}{\partial x} & 0 \\
0 & \displaystyle \frac{\partial N_1}{\partial y} & 0 & \displaystyle \frac{\partial N_2}{\partial y} & 0 & \displaystyle \frac{\partial N_3}{\partial y} \\
\displaystyle \frac{\partial N_1}{\partial y} & \displaystyle \frac{\partial N_1}{\partial x} & \displaystyle \frac{\partial N_2}{\partial y} & \displaystyle \frac{\partial N_2}{\partial x} & \displaystyle \frac{\partial N_3}{\partial y} & \displaystyle \frac{\partial N_3}{\partial x}
\end{array} \right] \tag{18}
\end{align}
三角形1次要素と違うのは、形状関数が\(\eta,\xi\)の関数であることである。このため、形状関数を\(x\)と\(y\)で直接微分することができない。そこで、\(B\)マトリクスを構成する成分\(\frac{\partial N_i}{\partial x}\),\(\frac{\partial N_i}{\partial y}\)を求めるための工夫が必要になる。
これらの成分は、微分の連鎖則を用いて、次式のように書き換えることができる。
\begin{align}\displaystyle\frac{\partial N_i}{\partial \xi} = \displaystyle\frac{\partial N_i}{\partial x}\displaystyle\frac{\partial x}{\partial \xi} + \displaystyle\frac{\partial N_i}{\partial y}\displaystyle\frac{\partial y}{\partial \xi} \\
\displaystyle\frac{\partial N_i}{\partial \eta} = \displaystyle\frac{\partial N_i}{\partial x}\displaystyle\frac{\partial x}{\partial \eta} + \displaystyle\frac{\partial N_i}{\partial y}\displaystyle\frac{\partial y}{\partial \eta} \tag{19} \end{align}
これをマトリクスで表現すると、
\begin{align} \left\{ \begin{array}{c} \displaystyle\frac{\partial N_i}{\partial \xi} \\ \displaystyle\frac{\partial N_i}{\partial \eta} \end{array} \right\} &= \left[ \begin{array}{cc} \displaystyle\frac{\partial x}{\partial \xi} & \displaystyle\frac{\partial y}{\partial \xi} \\ \displaystyle\frac{\partial x}{\partial \eta} & \displaystyle\frac{\partial y}{\partial \eta} \end{array} \right] \left\{ \begin{array}{c} \displaystyle\frac{\partial N_i}{\partial x} \\ \displaystyle\frac{\partial N_i}{\partial y} \end{array} \right\} \tag{20} \end{align}
となる。ここで、右辺第1項を、ヤコビ行列\(\left[J\right]\)とおく。
\begin{align} \left[J\right] &= \left[ \begin{array}{cc} \displaystyle\frac{\partial x}{\partial \xi} & \displaystyle\frac{\partial y}{\partial \xi} \\ \displaystyle\frac{\partial x}{\partial \eta} & \displaystyle\frac{\partial y}{\partial \eta} \end{array} \right] \tag{21} \end{align}
ヤコビ行列の逆行列を用いると、\(\left\{ \begin{array}{cc}\frac{\partial N_i}{\partial x} & \frac{\partial N_i}{\partial y} \end{array} \right\}\)についての式は、下式のように表される。
\begin{align} \left\{ \begin{array}{c} \displaystyle\frac{\partial N_i}{\partial x} \\ \displaystyle\frac{\partial N_i}{\partial y} \end{array}\right\} &= \left[J\right]^{-1} \left\{ \begin{array}{c} \displaystyle\frac{\partial N_i}{\partial \xi} \\ \displaystyle\frac{\partial N_i}{\partial \eta} \end{array} \right\} \tag{22} \end{align}
ここで、ヤコビ行列の逆行列は、
\begin{align} \left[J\right]^{-1} &= \displaystyle\frac{1}{\det\left[J\right]} \left[ \begin{array}{cc} \displaystyle\frac{\partial y}{\partial \eta} & -\displaystyle\frac{\partial y}{\partial \xi} \\ -\displaystyle\frac{\partial x}{\partial \eta} & \displaystyle\frac{\partial x}{\partial \xi} \end{array} \right] \tag{23} \end{align}
$$\det\left[J\right] = \displaystyle\frac{\partial x}{\partial \xi}\displaystyle\frac{\partial y}{\partial \eta} – \displaystyle\frac{\partial y}{\partial \xi}\displaystyle\frac{\partial x}{\partial \eta}$$
である。
これを整理すると、
\begin{align}
\displaystyle\frac{\partial N_i}{\partial x} &= \displaystyle\frac{1}{\det\left[J\right]}\left(\displaystyle\frac{\partial N_i}{\partial \xi}\displaystyle\frac{\partial y}{\partial \eta} – \displaystyle\frac{\partial N_i}{\partial \eta}\displaystyle\frac{\partial y}{\partial \xi}\right) \tag{24} \\
\displaystyle\frac{\partial N_i}{\partial y} &= \displaystyle\frac{1}{\det\left[J\right]}\left(-\displaystyle\frac{\partial N_i}{\partial \xi}\displaystyle\frac{\partial x}{\partial \eta} + \displaystyle\frac{\partial N_i}{\partial \eta}\displaystyle\frac{\partial x}{\partial \xi}\right) \tag{25} \end{align}
次に全体座標\(x,y\)を正規化座標\(\eta,\xi\)で偏微分する。全体座標を用いると、要素内の任意点の座標は、式(13)(14)より、
\begin{align} x &= N_1x_1 + N_2x_2 + N_3x_3 + N_4x_4 \tag{26} \\
y &= N_1y_1 + N_2y_2 + N_3y_3 + N_4y_4 \tag{27} \end{align}
と表すことができる。
これらの座標成分を正規化座標の成分\(\eta,\xi\)で偏微分する。
$$\left.\array{\begin{align}
\displaystyle\frac{\partial x}{\partial \xi} &=
\displaystyle\frac{\partial N_1}{\partial \xi}x_1 + \displaystyle\frac{\partial N_2}{\partial \xi}x_2 + \displaystyle\frac{\partial N_3}{\partial \xi}x_3 + \displaystyle\frac{\partial N_4}{\partial \xi}x_4 \\
\displaystyle\frac{\partial x}{\partial \eta} &= \displaystyle\frac{\partial N_1}{\partial \eta}x_1 + \displaystyle\frac{\partial N_2}{\partial \eta}x_2 + \displaystyle\frac{\partial N_3}{\partial \eta}x_3 + \displaystyle\frac{\partial N_4}{\partial \eta}x_4 \\
\displaystyle\frac{\partial y}{\partial \xi} &= \displaystyle\frac{\partial N_1}{\partial \xi}y_1 + \displaystyle\frac{\partial N_2}{\partial \xi}y_2 + \displaystyle\frac{\partial N_3}{\partial \xi}y_3 + \displaystyle\frac{\partial N_4}{\partial \xi}y_4 \\
\displaystyle\frac{\partial y}{\partial \eta} &= \displaystyle\frac{\partial N_1}{\partial \eta}y_1 + \displaystyle\frac{\partial N_2}{\partial \eta}y_2 + \displaystyle\frac{\partial N_3}{\partial \eta}y_3 + \displaystyle\frac{\partial N_4}{\partial \eta}y_4 \end{align}}\right\} \tag{28}$$
となる。
式(24),(25)に代入する値を求めるため、形状関数を正規化座標\(\xi\)で偏微分する。
$$\left.\array{\displaystyle\frac{\partial N_1}{\partial \xi} = \displaystyle\frac{\partial }{\partial \xi}\left\{\displaystyle\frac{1}{4}(1-\xi)(1-\eta)\right\} = – \displaystyle\frac{1 – \eta}{4}\\
\displaystyle\frac{\partial N_2}{\partial \xi} = \displaystyle\frac{\partial }{\partial \xi}\left\{\displaystyle\frac{1}{4}(1+\xi)(1-\eta)\right\} = + \displaystyle\frac{1 – \eta}{4}\\
\displaystyle\frac{\partial N_3}{\partial \xi} = \displaystyle\frac{\partial }{\partial \xi}\left\{\displaystyle\frac{1}{4}(1+\xi)(1+\eta)\right\} = + \displaystyle\frac{1 + \eta}{4}\\
\displaystyle\frac{\partial N_4}{\partial \xi} = \displaystyle\frac{\partial }{\partial \xi}\left\{\displaystyle\frac{1}{4}(1-\xi)(1+\eta)\right\} = – \displaystyle\frac{1 + \eta}{4}}\right\} \tag{29}$$
同様に正規化座標\(\eta\)で偏微分する。
$$\left.\array{\displaystyle\frac{\partial N_1}{\partial \eta} = \displaystyle\frac{\partial }{\partial \eta}\left\{\displaystyle\frac{1}{4}(1-\xi)(1-\eta)\right\} = – \displaystyle\frac{1 – \xi}{4}\\
\displaystyle\frac{\partial N_2}{\partial \eta} = \displaystyle\frac{\partial }{\partial \eta}\left\{\displaystyle\frac{1}{4}(1+\xi)(1-\eta)\right\} = – \displaystyle\frac{1 + \xi}{4}\\
\displaystyle\frac{\partial N_3}{\partial \eta} = \displaystyle\frac{\partial }{\partial \eta}\left\{\displaystyle\frac{1}{4}(1+\xi)(1+\eta)\right\} = + \displaystyle\frac{1 + \xi}{4}\\
\displaystyle\frac{\partial N_4}{\partial \eta} = \displaystyle\frac{\partial }{\partial \eta}\left\{\displaystyle\frac{1}{4}(1-\xi)(1+\eta)\right\} = + \displaystyle\frac{1 – \xi}{4}}\right\} \tag{30}$$
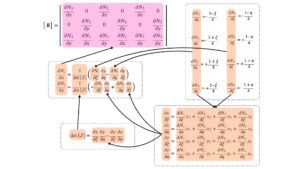
四角形1次要素の\(B\)マトリクスを計算するためには、これらの式が必要になる。かなり複雑な式の組み合わせであるので、式の関係を下図にまとめた。
⏬\(B\)マトリクスを計算するためのPythonコードを載せておく⏬
このPythonコードは、下記サイトの一部である。変数の定義や構造解析の全コードは、下記サイトに乗っている。
四角形1次要素応力解析のPythonコード
def make_B():
for e in range(0,elements):
x1 = x[connectivity[e][0]-1]
x2 = x[connectivity[e][1]-1]
x3 = x[connectivity[e][2]-1]
x4 = x[connectivity[e][3]-1]
y1 = y[connectivity[e][0]-1]
y2 = y[connectivity[e][1]-1]
y3 = y[connectivity[e][2]-1]
y4 = y[connectivity[e][3]-1]
for ip in range(0,integral_points):
xi = ip_xi[ip]
et = ip_et[ip]
dN1dXi = - (1 - et) / 4
dN2dXi = (1 - et) / 4
dN3dXi = (1 + et) / 4
dN4dXi = - (1 + et) / 4
dN1dEt = - (1 - xi) / 4
dN2dEt = - (1 + xi) / 4
dN3dEt = (1 + xi) / 4
dN4dEt = (1 - xi) / 4
dXdXi = dN1dXi*x1 + dN2dXi*x2 + dN3dXi*x3 + dN4dXi*x4
dXdEt = dN1dEt*x1 + dN2dEt*x2 + dN3dEt*x3 + dN4dEt*x4
dYdXi = dN1dXi*y1 + dN2dXi*y2 + dN3dXi*y3 + dN4dXi*y4
dYdEt = dN1dEt*x1 + dN2dEt*x2 + dN3dEt*x3 + dN4dEt*x4
detJ[e][ip] = dXdXi * dYdEt - dXdEt * dYdXi
dN1dX = (dN1dXi * dYdEt - dN1dEt * dYdXi) / detJ[e][ip]
dN2dX = (dN2dXi * dYdEt - dN2dEt * dYdXi) / detJ[e][ip]
dN3dX = (dN3dXi * dYdEt - dN3dEt * dYdXi) / detJ[e][ip]
dN4dX = (dN4dXi * dYdEt - dN4dEt * dYdXi) / detJ[e][ip]
dN1dY = ( - dN1dXi * dXdEt + dN1dEt * dXdXi) / detJ[e][ip]
dN2dY = ( - dN2dXi * dXdEt + dN2dEt * dXdXi) / detJ[e][ip]
dN3dY = ( - dN3dXi * dXdEt + dN3dEt * dXdXi) / detJ[e][ip]
dN4dY = ( - dN4dXi * dXdEt + dN4dEt * dXdXi) / detJ[e][ip]
B[e][ip][0][0] = dN1dX
B[e][ip][0][1] = 0.0
B[e][ip][0][2] = dN2dX
B[e][ip][0][3] = 0.0
B[e][ip][0][4] = dN3dX
B[e][ip][0][5] = 0.0
B[e][ip][0][6] = dN4dX
B[e][ip][0][7] = 0.0
B[e][ip][1][0] = 0.0
B[e][ip][1][1] = dN1dY
B[e][ip][1][2] = 0.0
B[e][ip][1][3] = dN2dY
B[e][ip][1][4] = 0.0
B[e][ip][1][5] = dN3dY
B[e][ip][1][6] = 0.0
B[e][ip][1][7] = dN3dY
B[e][ip][2][0] = dN1dY
B[e][ip][2][1] = dN1dX
B[e][ip][2][2] = dN2dY
B[e][ip][2][3] = dN2dX
B[e][ip][2][4] = dN3dY
B[e][ip][2][5] = dN3dX
B[e][ip][2][6] = dN4dY
B[e][ip][2][7] = dN4dX
-数値積分と積分点
\(B\)マトリクスを求めた後は、次式の要素剛性マトリクスを求める。
$$\left[\mathbf{K_e}\right]\equiv\int_V\left[\mathbf{B}\right]^T\left[\mathbf{D}\right]^T\left[\mathbf{B}\right]dV\tag{31}$$
\(B\)マトリクスは形状関数の1階微分なので、それを積分することで形状関数と物理的な意味は同じになる。つまり、要素剛性マトリクスは、要素内の変位分布を表現する関数である。\(B\)マトリクスは、要素内の座標によって異なる値となるが、要素剛性マトリクスは、要素内で同じ値となる。
この節では、式(31)を積分する手法を解説していく。
FEMでよく用いられているプログラム言語は、高校数学で習うような解析的な積分が極めて苦手である。そこで誕生したのが、数値積分である。最近のFEMでは、ガウスの公式を使用して数値積分することが普通である。
数値積分の基本的な考え方は、下記のような3つの流れである。
① 積分区間をいくつかの小区間に分ける。
② 各小区間の関数を単純な関数で近似する。
③ 近似した単純な関数を積分することによって近似値を求める。
数値積分をする上で、欠かせない概念が「積分点」である。積分点とは、小区間内の単純な関数を積分するために使用する点である。
「ガウスの公式」と「積分点」について、詳細に見てみよう。
ガウスの公式
まずは、下図のような1次元の関数に対して、ガウスの公式を適用してみる。分かりやすいように積分区間を\(-1\le x\le 1\)とする。これは、四角形1次要素で解説したような正規化座標と考えてほしい。今回は、積分点を2つ用いたガウスの2点公式について解いていく。
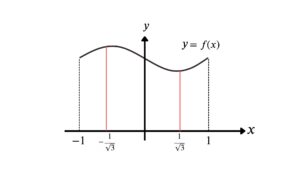
図に示したように、ガウスの2点公式では積分点は\(-\frac{1}{\sqrt{3}}\)と\(\frac{1}{\sqrt{3}}\)である。この積分点の座標は、積分点の数によって決められている。小区間内を数値積分すると、積分点と関数\(y = f(x)\)を用いて、次式で表される。
$$\displaystyle \int_{-1}^{1}f(x)dx = \displaystyle\sum_{i=1}^{n}w_if(x_i)\tag{32}$$
ただし、\(i\)は積分点の番号、\(w_i\)は積分点の重みを意味する。積分点の重みも、積分点数と積分点座標によってあらかじめ決められている。ガウスの2点公式の場合は、重みは2つの積分点で同じ\(w_i =1\)である。実際にガウスの公式を用いて数値積分したイメージが下図である。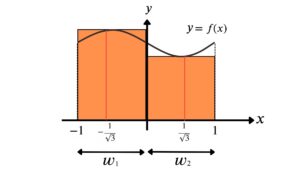
四角形1次要素でのガウスの公式
四角形1次要素の要素剛性マトリクスは、次式で算出できる。
$$\left[\mathbf{K_e}\right]=\int\int\int\left[\mathbf{B}\right]^T\left[\mathbf{D}\right]^T\left[\mathbf{B}\right]dxdydz\tag{33}$$
これを正規化座標で置き換えると、
$$\displaystyle\left[\mathbf{K_e}\right]=t\int_{-1}^1\int_{-1}^1\left[\mathbf{B}\right]^T\left[\mathbf{D}\right]^T\left[\mathbf{B}\right]\left|J\right|d\xi d\eta\tag{34}$$
ここで、\(\left|J\right|\)は、全体座標系と正規化座標系の変換行列\(\left[J\right]\)の行列式である。\(\left|J\right|\)を乗じることで、全体座標系と正規化座標系の面積を変換していると理解することができる。\(t\)は、\(z\)方向が一定で、\(z\)成分の積分を厚さ\(t\)の積で置換している。
式(32)と同様に、ガウスの公式を適用する。2次元の場合のガウスの公式は、次式となる。
$$\displaystyle\int_{-1}^1\int_{-1}^1f(\xi,\eta)d\xi d\eta = \sum_{i=1}^{n} \sum_{j=1}^{n}w_iw_jf(\xi_i,\eta_j)\tag{35}$$
式(34)に式(35)を適用すると、
\begin{align*}
\displaystyle\left[\mathbf{K_e}\right]
&=t\int_{-1}^1\int_{-1}^1\left[\mathbf{B}\right]^T\left[\mathbf{D}\right]^T\left[\mathbf{B}\right]\left|J\right|d\xi d\eta\\
&= t\sum_{i=1}^{n}\sum_{j=1}^{n}w_iw_j\left[\mathbf{B}\right]^T\left[\mathbf{D}\right]^T\left[\mathbf{B}\right]\left|J\right|\tag{36}\end{align*}
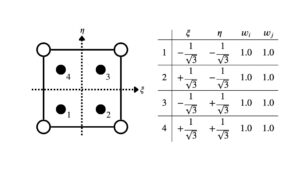
四角形1次要素の積分点の数とその座標\(\xi_i,\eta_i\)、積分点の重み\(w_i,w_j\)は、下の表の通りである。
 実際に四角形1次要素を数値積分したイメージが下図である。
実際に四角形1次要素を数値積分したイメージが下図である。
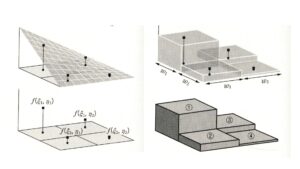 \(\left|J\right|\)と\(\left[B\right]\)は、\(\xi_i,\eta_i\)の関数である。また、\(w_i = w_j = 1\)であるので、式(36)を書き換えると、次式になる。
\(\left|J\right|\)と\(\left[B\right]\)は、\(\xi_i,\eta_i\)の関数である。また、\(w_i = w_j = 1\)であるので、式(36)を書き換えると、次式になる。
$$\displaystyle\left[\mathbf{K_e}\right]=t\sum_{i=1}^{2}\sum_{j=1}^{2}\left[\mathbf{B}(\xi_i,\eta_i)\right]^T\left[\mathbf{D}\right]^T\left[\mathbf{B}(\xi_i,\eta_i)\right]\left|J(\xi_i,\eta_i)\right|\tag{37}$$

